32   PRINCIPLES OF ELEMENTARY DYNAMICS

make one complete vibration. At the time t = 12, the angular

displacement 0 is proportional to the distance B'b'. The angular amplitude c is proportional to the distance Yd'.

The wave form due to a simple harmonic vibration is a sine curve (or cosine curve).

24. Phase and Phase Angle. - In the case of vibrations along a horizontal line, forces, velocities, currents, etc., directed to the right are usually termed positive; and displacements to the right of the equilibrium point are termed positive. In the case of vibrations along a vertical line, forces, currents, etc., directed upward are usually termed positive; and displacements above the equilibrium point are called positive. The phase of any periodically changing function is the fraction of a whole period of vibration which has elapsed since the particular function last passed the equilibrium position in the positive direction. Thus, if, in Fig. 21, a body vibrates along the line YY' with simple harmonic motion, and if, at intervals of one-twelfth of the period of vibration, the body is successively in the positions a, b, c, d, e, f, g, h, i, j, k, 1, a, etc., the phase of the displacement of the body when at a is zero; when at c and moving in the positive direction, the phase is' ; when at d, the phase is 4 7 when at c and moving in the negative direction the phase is 3i when at a and moving in the negative direction it is '2, etc.

If a body is rotating in a circle, the angular displacement of the body from some reference position is called the phase angle of the motion. Thus, in Fig. 21, when the point P is at B, the phase of

the displacement is 1'2 and its phase angle is 6 radians, or 30°; when at D the phase is 4 and its phase angle is 2 radians, or 90°. Since

the motion on a straight line of the projection of a point that is moving with uniform speed in the circumference of a circle is a simple harmonic motion of translation, we may express phase in terms of the phase angle of a point that is moving in the circumference of a circle. Thus, in Fig. 21, when the body is at b, and moving in the positive direction, the phase of the motion is I2 and

its phase angle is 6 radians or 30°. In the equations of Art. 20, the angle 0 P2T7rt1 represents the phase angle of the vibration at the time t   J.

SIMPLE HARMONIC MOTION   33

Two motions having phase angles that differ by zero or by any integral multiple of 2 7r radians are said to be in the same phase. Two motions having phase angles that differ by ,7r radians are said to be in opposite phases. In Fig. 21, the properties corresponding to b' and b" are in the same phase, and those corresponding to d' and d" are in the same phase. The properties corresponding to d' and j are in opposite phase.

25. The Mean Value of the Product of Two Simple Harmonic Functions of Equal Period. - There are many cases in which it is necessary to know the mean value of the product of two quantities that are varying periodically. If, at any instant, a body rotating with an angular speed w exerts a torque L, the power developed at that instant equals wL. If the torque and the angular speed are varying periodically, the mean power developed during one cycle equals the average of a series of products of w and L during the cycle.

Similarly, the mean power associated with an alternating electric current during one cycle equals the average of a series of products of instantaneous values of electromotive force and current during the cycle.

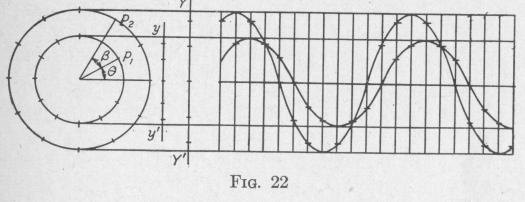
The most important case is that in which the two periodic quantities vary harmonically and are of the same period. Assume two simple harmonic motions represented, respectively, by the equations

di = r, sin B and d2 = r2 sin (0 + 3)

where r, and r2 are the amplitudes of vibration, d, and d2 are the displacements from the equilibrium position, and 0 and (0 + 0)

are the phase angles at the time t. Since the periods are the same, Q is independent of time. In Fig. 22, the displacements of the two vibrations at the end of a series of equal time intervals are indicated by dots on the lines yy' and YY', respectively. The wave