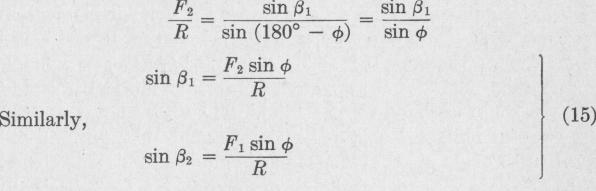ems of forces having identical effects on the motion oa oy are aid to be equivalent. A single force equivalent to two or more imultaneous forces is called the resultant of the set. Two forces which, acting together, are equivalent to a single force are called omponents of the given force. The operation of finding the re- sultant of a system of forces is called composition of forces.
The method of finding the resultant of two concurrent forces, called the parallelogram law, may be stated as follows: If two adjacent sides of a parallelogram represent in direction and in mag- nitude two concurrent forces, both directed from the point of inter- section, then the diagonal of the parallelogram drawn from this
intersection represents completely, in direction and in magnitude, the re- sultant of the two forces.
If the magnitudes of the two concurrent forces be represented by F, and F2, Fig. 2, and if the angle between them be 0, then
from the law of cosines the magnitude of the resultant R is given by the equation
Fly and Fv, Fig. 6. If H and V are at right angles to one another, Fg = F cos 0 and Fv = F sin 4.
A force may be resolved into three components in assigned directions. For instance, the components may be found in the vertical, in the north-south, and in the east-west directions.
V
Linear veocities, near accelerations, and linear momenta can be completely represented by directed straight lines as can forces. The parallelogram law, used for forces, can also be used to com-
By compounding the resultant of two concurrent forces with a third force that is concurrent with this resultant, we can find the resultant of all three forces.
The operation of finding the components in two given directions of a force is called resolution of the force. The components of the force F, Fig. 3, in the directions A and B, Fig. 4, are FA and FB, Fig. 5; the components in the directions H and V, Fig. 4, are
The angle between the line representing either one of the component forces and the line representing the resultant can be obtained from Fig. 2 and the law of sines,
pound and resolve these quantities. However, since all velocity is relative to some reference body, care must be exercised to keep clearly in mind what object is moving and what object is taken as the body of reference. One method by which this can be done easily is illustrated in the following Article.
4. Composition and Resolution of Uniform Linear Velocities and Accelerations. - A passenger moving across a moving railway carriage furnishes an example of what are called simultaneous velocities. The passenger has a velocity relative to a point of the carriage, and at the same time the carriage has a velocity with respect to a point on the earth. These are called components of the passenger's motion. The velocity of the passenger with reference to the earth is called his resultant velocity.
In order that we may keep clearly in mind what object is re-
PRINCIPLES OF ELEMENTARY DYNAMICS
TRANSLATION AND ROTATION