182 NAVIGATIONAL COMPASSES
§2. The Natural Errors to which the Gyro-Compass is Subject
110. The Latitude Error. - Owing to the rotation of the earth, combined with the tendency of the spin-axle of a gyroscope to maintain its direction in space, the end of the axle of a gyro-compass moves back and forth across the meridian plane and also up and down across the horizontal plane through the center of the gyro-wheel (Arts. 106, 107). If the gyro-compass is north of the equator and if the gyro-axle is horizontal and pointing east of the meridian plane, the north-seeking end of the spin-axle will rise and move westward. The tilting of the spin-axle is necessary for the production of the torque required to cause the gyro-axle to seek the meridian. At any latitude the tilt of the spin-axle of an undamped compass, when the axle is in the meridian plane, is just sufficient to produce the rate of precession about a vertical axis required to maintain the axle in the meridian.
Any damping action that opposes the natural tilting of the spinaxle will result in a lower rate of precession than that required to maintain the axle in the meridian. The resting position of the spin-axle will then be deviated from the meridian plane by an angle called the latitude error or the damping error. If the method used for damping does not involve an opposition to tilting of the gyroaxle, then there will be zero latitude error. When there is latitude error, its magnitude depends upon the latitude and upon the constants of the compass. The Florentia and the Sperry gyro-compasses are subject to a latitude error. This latitude error is compensated automatically by a device that forms part of the compass.
111. The Error Due to the Velocity of the Ship. The MeridianSteaming Error. - A gyro-compass on board a ship at sea is subject to deflecting forces due to the motion of translation of the ship and also to angular motions of steering, rolling and pitching. The deflection of the spin-axle from the meridian due to the linear velocity of the ship will now be considered.
Suppose that the ship is moving with a linear velocity vs on a course inclined at an angle B to the meridian. Then the component in the direction of the meridian is vs cos B. The angular velocity of the ship with respect to the earth about an east-and-west axis has the value
vs cos 0
ews = R
where R represents the radius of the earth.
NATURAL ERRORS 183
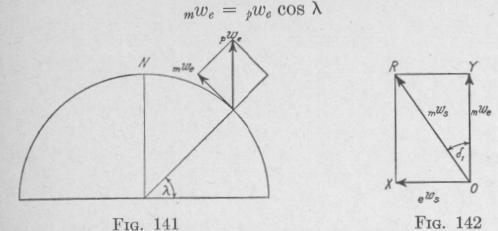
If we represent the angular velocity of the earth about its axis, with respect to some fixed line in space, by pwe, then the component angular velocity of the earth relative to a horizontal axis in the meridian plane at a place of latitude X (Fig. 141) is
In Fig. 142, the two angular velocities ews and mwe are represented by the lines OX and O Y, respectively. The resultant angular velocity of the ship with respect to a horizontal axis in the meridian plane, .ws, is represented by OR. The spin-axle of the gyro-compass sets itself parallel to the axis of the resultant angular velocity of the ship. In this figure
tan S, = -e = Ryw os X
(118
This deflection, S,, called the meridian or north-steaming error, is westerly for a northern course, and easterly for a southern course. It is independent of the construction of the compass. In Art. 113 it will be shown how the appropriate meridian-steaming deflection can be produced, without oscillation, just as soon as any change occurs in either the speed or the course of the ship.
If the linear speed of the ship be expressed as v knots, then
vs = 6080 v ft. per hour. R = 20,925,000 ft.
pwe = 1 rev. per day = 24 radian per hour = 0.26 rad. per hour. Hence,
6080 feet per hour v cos 0 tan S, _ (20,925,000 ft.) (0.26 rad. per hr.) cos X
Neglecting the small difference between 5, and tan S,, and remembering that 1 radian = 57.3 degrees, we have the value of the meridian-steaming error:
S, = 0.0011 co sA radians = 0.063 co sA degrees (119)