GENERAL PRINCIPLES 257
In the present case, the torque due to gravity is in the same direction as the gyroscopic torque which was developed by the push and which produced an angular acceleration about the axis cc'. The torque acting on the system is, (Art. 69)
z
L,' = mgHO - 2w
The direction of the resultant torque depends upon the value of 0. This system is dynamically stable when
K52ws20 > mgHO
Kc
Multiplying each side of this inequality by 2Ks, we see that the
condition of dynamical stability assumes the form: KSw52 K, mgH 2 > KS 2
The left-hand side of this inequality represents the kinetic energy of rotation of the gyro-wheel. The quantity within the parenthesis represents one-half of the change in the potential energy of the system in falling through the distance H. Thus, an oscillating system that is statically unstable can be rendered dynamically stable by means of a statically unstable gyroscope capable of precessing about an axis perpendicular to the axis of oscillation of the system, if the kinetic energy of rotation of the gyro-wheel is greater than K,/ K, times one-half of the potential energy lost by the system in rotating about the axis of oscillation from a vertical position to a horizontal position.
This principle is the basis of all methods proposed for stabilizing monorail cars.
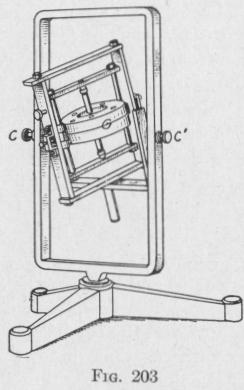
156. Some Laws of Dynamic Stability. - There are several laws of dynamic stability to which we shall need to refer in subsequent considerations. The following can be proved by analytic methods and can be illustrated readily by the apparatus shown in Fig. 203.
(a) If the inner frame and spinning wheel of a gyroscope be statically stable with respect to a horizontal axis perpendicular to the spin-axle, and if at the same time the second frame be also statically stable with respect to a horizontal axis perpendicular to the first, then the system will be dynamically stable and the two axes will precess in the direction opposite the spin (Art. 155, a).
256 GYROSCOPIC STABILIZATION
(a) A Statically Stable Gyro on a Statically Stable Body Capable of Oscillation under the Influence of Gravity. - When the ampli- tude of oscillation 0 is small and the gyro-wheel is not spinning, the equation of motion of the system of mass m is
2
mk2 dt2 = -mgHB (131)
where t is the time occupied in moving through the angle B.
If the gyro-wheel is spinning, there is an additional torque
acting on the system (Art. 69) in the same direction as that due
to gravity. When the spin-axis is perpendicular to the axis of oscilla- tion, the equation of motion of the system is (90) and (131),
L,' _ -mgHO - K'2w'20 (132)
K,
where K, represents the moment of
inertia of the gyroscope with respect
to the axis about which the system
oscillates.
Since no change of the magnitude
of B produces a reversal of the direc-
tion of the resultant torque acting
on the system, it follows that the
system is not only statically stable
but also always dynamically stable.
(b) A Statically Unstable Gyro on a Statically Unstable Oscil- lating Body. Experiment. - Figure 203 represents a system in- cluding a gyro-wheel G that can either hang pendulously and oscil- late about a rod cc' or can be turned into the position shown in the figure with the center of gravity above the axis of support. When in the position shown in the figure, if the system be slightly dis- placed about the axis cc' while the wheel is not spinning, the system will continue to rotate for 180 degrees till the center of gravity is below the line cc'. The system is sometimes called a stilt top or inverted gyroscopic pendulum. It is statically unstable when in the position shown.
With the gyroscope anti-pendulous and the entire system un- stable, set the gyro-wheel spinning. Now push on the gyro-frame, thereby producing a small displacement about the axis cc'. The system does not flop over. It is dynamically stable.