28 PRINCIPLES OF ELEMENTARY DYNAMICS
If the angular amplitude, expressed in degrees, be represented by V, (45) gives
° °
we T 57,3 rad. per sec. = 912 T rad. per sec. (46)
Angular Displacement. If a body is vibrating with simple harmonic motion of translation of period T and amplitude r, the linear displacement from the equilibrium position t seconds after traversing the equilibrium position has the value, Fig. 18:
d = r sin B = r sin 2T t = r cos l 2 - _T t) (47)
From (43), we find that when a body has a simple harmonic motion of rotation with period T and amplitude 4~, the angular displacement from its equilibrium position at time t is given by the expression
¢ _ 4) sin 0 = 4) sin 2Tt = cos \2 - 2T t\ (48)
21. The Physical Pendulum. - A compound or physical pen
dulum consists of a suspended rigid body free to oscillate about a
horizontal axis. Consider the physical pendulum
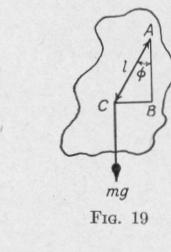
AC (Fig. 19), consisting of a body of mass m supported on an axis normal to the plane of the diagram and passing through the point A. Let the center of gravity of the pendulum be at C. Denote the distance AC by 1. If the pendulum be deflected from its equilibrium position through an angle 0, it will be acted upon by a torque which tends to restore it to the equilibrium position and which has a value
L = -mg(BC) _ - mgl sin h
the negative sign indicating that the direction of the torque is opposite that of the displacement.
If the displacement from the equilibrium position is small, sin 0 is approximately equal to ¢ radians. In this case the above equation becomes
L = -mgl 0 (49)
Whence, at any instant, a pendulum displaced but a small distance from its equilibrium position is urged toward its equilibrium
SIMPLE HARMONIC MOTION 29
position by a torque nearly proportional to its angular displacement from that position. Consequently, the angular motion of such a pendulum is approximately simple harmonic motion of rotation.
The period of vibration of a physical pendulum oscillating through a small amplitude now will be determined. Substituting in the equation for the period of vibration of a simple harmonic motion of rotation, (37), the value of the torque acting on a compound pendulum displaced through a small angle 4 from its position of equilibrium, (49), we obtain for the value of the time occuied bone comlete vibration of a comound endulum:
From this equation it is seen that when the amplitude of vibration of a compound pendulum is so small that sin 0 may be replaced by 0, the period of vibration of the pendulum is practically independent of the amplitude of swing.
A heavy particle suspended by a string which is both inextensible and massless, and which is capable of swinging in a vertical plane, is called a simple or mathematical pendulum. Since the moment of inertia with respect to the axis of oscillation of a simple pendulum of length 1 and mass m is (21):
K=m12
The eriod of vibration of a simle pendulum is (50):
A pendulum consisting of a small spherical bob supported by a very thin light inextensible string approximates closely to a simple pendulum.
A rigid body free to oscillate about a horizontal axis that is below the center of mass of the body is called an inverted pendulum. One type of seismograph for recording earth tremors consists of an inverted pendulum having the upper end normally held in position by a set of springs.
22. The Conical Pendulum. - If a body, suspended at a point not coincident with the center of mass of the body, be given an impulse directed to one side of the vertical line through the point of suort, each line of the body passing through the point of