36   PRINCIPLES OF ELEMENTARY DYNAMICS

the power curve and the axis, for any time interval, is proportional to the work done during the given interval. An area above the axis represents positive work, that is work done by the electromotive force or by the torque; an area below the axis represents negative work, that is work done against the electromotive force or against the applied torque. When the two harmonic curves are of equal period and in quadrature, that is, when they

differ in phase by 2 radians or 90°, Fig. 24, the total work done

during one cycle is zero.

The quotient obtained by dividing the area under the power curve for one-half cycle, by the distance between the intersections of this curve with the axis of the curve, equals the mean value of the power during the half cycle. When the two curves are in quadrature, Fig. 24, the mean power during a complete cycle is zero.

The phase difference between the current and the electromotive force in an alternating current circuit can be altered by changing either the capacitance or the inductance of the circuit. If the current and the electromotive force in a circuit containing an alternating current generator and motor are in the same phase, then the generator is putting electric energy into the line and the motor is transforming a maximum fraction of it into mechanical work. If the current and electromotive force differ in phase by one-quarter period, then we have a " wattless current " and the work done during one complete cycle is zero. If the current and the electromotive force are in opposite phase, then the motor is operating as a generator, opposing the electromotive force of the generator.

26. Oscillations of a Coupled System. Resonance. - The vibrations executed by a body which has been displaced from its position of equilibrium and then released are called free vibrations. The vibrations executed under the action of an external periodically varying force are called forced vibrations.

If the point of support of a vibrating pendulum is in periodic motion, as when a pendulum is attached to another pendulum, or when a pendulum is on a ship which is rolling with a constant period, the pendulum will acquire a compound periodic motion having two components of different periods. These periods will be different from the periods of the freely vibrating pendulum or of the freely vibrating support, except when the inertia of the pendulum is negligible compared with the inertia of the support.

SIMPLE HARMONIC MOTION

The amplitude of the component oscillation of shorter period will be smaller than the amplitude of the component oscillation of longer period.*

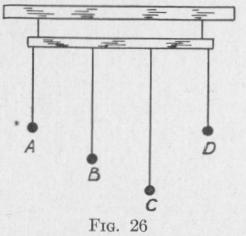
Consider a group of pendulums hung from a horizontal rod supported as shown in Fig. 26. Suppose that the pendulum A is set swinging. When it is out on one side of its path it urges the

supporting rod out toward that same side. When it is out on the other side of its path it urges the support out toward that side. The force acting on the support varies harmonically. Soon the support and the other pendulums are set into forced vibration of nearly the same frequency as the free vibration frequency of the exciting pendulum A.

If the length of the pendulum A is so much greater than the lengths of the other pendulums that the frequency of the forced vibration is much less than the natural vibration frequency of these pendulums when vibrating freely, then they will vibrate with the frequency of the forced vibration. If the frequency of the forced vibration be increased by shortening the length of the exciting pendulum A, for example, the amplitude of the vibration of the other pendulums will increase. If the frequency of the forced vibration equals the natural frequency of some pendulum D, then this pendulum will be acted upon by the maximum force in the direction of its motion when it is moving through its equilibrium position. Consequently, the amplitude of vibration of D will become large. The vibration produced when a periodically varying force acts upon a body of nearly the same frequency of vibration is called resonant forced vibration. The phenomenon of the production of resonant forced vibrations is called resonance. The body that excites the resonance is called the exciter, and the one that is set into resonant forced vibration is called the resonator. The frequency of the external force that produces maximum resonance is called the critical frequency.

Resonance is a very important phenomenon in mechanics as well as in electricity, sound and light. Some of the more important aspects of the phenomenon that relate to mechanics are broadly indicated in the present considerations.

* Edser, General Physics for Students, pp. 154-167.