46   MOTION OF A SPINNING BODY

axis perpendicular to the spin-axle, the spin-axle rotates with constant angular velocity wp about an axis perpendicular to both the spin-axis and the torque-axis.

An outside torque acting upon an unconstrained spinning sym

metrical body about the spin-axis changes the magnitude of the

spin-velocity but not the direction of the spin-axis. An outside torque acting about an axis perpendicular to the spinaxis does not change the magnitude of the spin-velocity but does change the direction of the spin-axis in the manner now to be explained. The cause of the oscillations of the spin-axle before a steady state is attained will be considered in Art. 39.

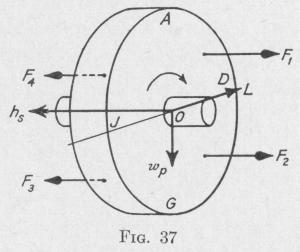
We shall use two different methods of explanation. In the first method, we shall consider a symmetrical wheel, Fig. 36, spinning with angular velocity w, about the axle of the wheel, and also rotating with angular velocity wp about an axis perpendicular to the spin-axis. The resultant of these two angular veloci

ties is an angular velocity represented in magnitude, direction of

axis and sense of rotation by the arrow labeled w,.

Each particle of the wheel is moving in a circular path about

some point on the axis of w, as

a center. In order that this

motion may continue, each par

ticle must be acted upon by a

force directed toward the center

of its circular path (Art. 9). The

centripetal forces acting on two

particles A and A' situated at

points equally distant from the

axis of the resultant angular ve

locity w„ are represented by the

arrows f and f. These two forces constitute a couple acting in the counter-clockwise direction about an axis perpendicular to the axes of w, and wp. The sum of the centripetal couples that must act upon all the particles composing the spinning body consti

MOTION OF A SPINNING BODY   47

tutes a resultant centripetal torque L. A torque of this value must be applied to the spinning body by an outside agent in order that the body may rotate with angular velocity wp about an axis perpendicular to the spin-axis.

If such a centripetal torque be not applied by some outside agent, the inertia of each particle of the spinning body will cause it to move tangentially to its circular path and the wheel will not turn about any axis except the spin-axis. In case the face of the wheel were not perpendicular to the spin-axis, a torque would act upon the wheel tending to set the face of the wheel perpendicular to the spin-axis. The magnitude of this torque equals the centripetal couple required to hold the wheel inclined to the spin-axis.

Any rotating body tends to set

itself so that its axis of maximum moment of inertia is in the direction of the axis of rotation.

In the second method of ex

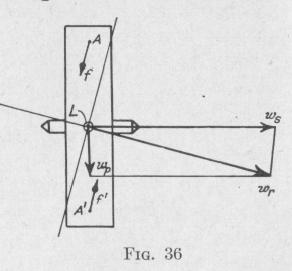
planation, we shall assume that the wheel in Fig. 37 is spinning at a constant rate in the direction indicated and, at the same time, is turning at a constant

rate about the axis JD in the direction of an external torque L of constant magnitude. Owing to the resultant of these two motions, particles in the quadrant OAD and in the quadrant OGJ are approaching the axis JD while particles in the quadrants ODG and OJA are receding from this axis.

When a particle approaches the axis JD, its moment of inertia relative to that axis decreases. Since the rate of spin is constant, the angular speed of each particle about the axis JD increases when the particle is approaching this axis. The angular motion about the axis JD of each particle in the quadrant OAD is accelerating toward the reader about the axis JD, while the motion of each particle in the quadrant OGJ is accelerating away from the reader. Thus, each particle in the quadrant OAD is acted upon by an external force directed toward the reader, while each particle in the quadrant OGJ is acted upon by a force directed away from the reader.

When a particle recedes from the axis JD, its moment of inertia relative to that axis increases. The rate of spin being constant, the