54   MOTION OF A SPINNING BODY

of the spin-velocity by w,, the moment of inertia of the wheel with respect to the spin-axis by K,, and the torque due to the added weight by L.

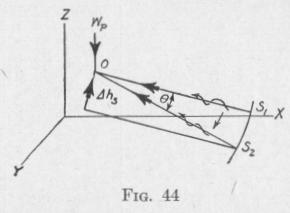
In Fig. 44, the angular momentum of the gyro-wheel about the

spin-axis at one instant is represented by the line 510, and at a

short interval of time At afterward by the line $20. During this time interval there has been a small change of angular momentum represented by the line S2S1 perpendicular to the spinaxis.

The time rate of change of angular momentum, that is the

torque required to maintain the constant precessional velocity wp

of a body spinning with angular velocity w, about an axis per

pendicular to the spin-axis and to the axis of precession, has the

value (28)

S2S1

L = At

Now during the short time interval At, the vertical plane through the spin-axis has rotated about a vertical axis through an angle 0 with a constant precessional velocity wp. Consequently, 0 = wp At. For a sufficiently short time interval, the chord S2S1 is approximately equal to the arc S2S1. Consequently,

6 [ S20] = WP At or S2S1= (S20)wp At

Substituting this value of S2S1 in the equation of torque,

L [= as 1] = (S20)wp

Remembering that the angular momentum represented by S20 has the magnitude K,w,[= h,], we find that the torque required to maintain a constant velocity of precession about an axis perpendicular to the spin-axis has the value

L[= (S20)wp] = K,w,wp= h,wp   (55)

where h,[= K,w,] is the angular momentum of the body relative to the spin-a4,L

MOTION OF A SPINNING BODY   55

The value of the torque required to maintain constant precession about an axis that is not perpendicular to the spin-axis is deduced in Art. 53.

Since for every torque there is a reacting torque of the same magnitude about the same axis acting upon a different body, it follows that if a body spinning with an angular speed w, rotates about another axis with angular speed wp there is developed a reacting torque acting on the restraints having a value L given by (55). The opposition which the axle of a rotating wheel offers to being turned about the axis of an applied torque is called the

gyroscopic couple, gyroscopic resistance, or the stabilizing property of the gyroscope.

From (55) it is seen that

(a) If the torque L be zero, then the precession will be zero. For example, if a wheel is mounted so as to be free to move about any axis passing through its center of mass, then the spin-axle remains fixed in space however the frame may be displaced. This

is the First Law of Gyrodynamics.

(b) When a constant torque L is acting on an unconstrained symmetrical spinning body about an axis perpendicular to the spinaxle, the spin-axis will precess steadily about an axis perpendicular to both the spin-axle and the torque-axis with an angular velocity

This is the Second Law of Gyrodynamics.

(c) When precession is prevented, that is, when wp = 0, then the torque L = 0. Hence, a rotating body offers zero opposition to a rotation of the axis of spin when precession is prevented.

35. The torque L produces an angular displacement about an axis perpendicular to the torque-axis, but may produce zero displacement about its own axis. Under these conditions, the torque does zero work. This is similar to the fact that a centripetal force acting perpendicular to the direction of the motion of a body moving in a circular path does no work on the body. -

Rotating dynamo or motor armatures, and the rotors of steam turbines, mounted lengthwise of a ship, develop on the ship considerable torques when the ship pitches, but not any when the ship rolls. If the axes of rotation be athwartship, there will be torques when the ship rolls, but not any when it pitches. With the mount-