62   MOTION OF A SPINNING BODY

perpendicular to the spin-axle, the spin-axle tilts in the direction of the torque. If the gyro is spinning and is unconstrained, the spin-axle precesses. This precession develops an internal torque that opposes the tilt which would occur if there were no precession.

About 1875 Sir Henry Bessemer organized a company to build a steamer to carry passengers across the English Channel without the discomfort of sea-sickness. Within the steamer was a large cabin weighing 180 tons mounted so as to be capable of oscillation about the fore-and-aft axis of the ship. A large wheel was mounted so as to spin about a fixed axis perpendicular to the floor of the cabin. The inventor assumed that the spin-axle would maintain its vertical position and thereby maintain the floor of the cabin nearly horizontal however the ship might roll. The device failed because the wheel was mounted so that it could not precess. Later, Schlick attained some success in preventing excessive roll

of a ship by means of a large wheel spin

ning about an upright axis and capable of precessing about an athwartship axis (Art. 90).

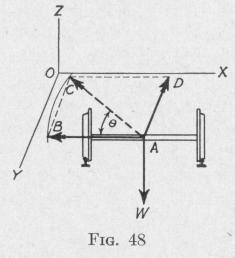
Consider a pair of car-wheels, with the connecting axle, moving around a horizontal curve. Let the angular momentum hs of the system with respect to the axle at any instant be represented by the line AB, Fig. 48, and the equal angular momentum at a short

time At, afterward by AC. If the angular velocity about a vertical

axis due to the motion around the curve be w, then the angle 0

through which the axle turns in time At is

0 = w At

The change in the angular momentum of the body, represented by the line AD, has the magnitude,

hsO = hsw At

and the time-rate of change of angular momentum, or the gyroscopic torque acting on the spinning body about the axis AD, in the clockwise direction, has the magnitude

L[= hsw] = Kswsw   (58)

The reaction of this torque, that is the torque developed by a spinning body of angular momentum h2, when turned with angular

MOTION OF A SPINNING BODY

velocity w about an axis perpendicular to the axes of hs and w acts in the opposite direction with the same magnitude on th( body that causes the change in the direction of the spin-axle:

L'[= hsw] = Kswsw   (59

In the case of a car going around a curve, this reaction tends to rotate the car away from the center of the curve.

If the spin-axle is not perpendicular to the axis about which the spin-axle is turning, the torque is perpendicular to the axis of turning and to the component of the spin-velocity perpendicular to the axis of turning.

If ws and w are of the same sign, the torque will be positive; if they are of opposite signs, the torque will be negative.

Problem. The shaft with the propeller of a certain torpedo boat has a moment of inertia of 2000 lb.-ft.2 with respect to the axis of the shaft. When the shaft is rotating at an angular speed of 300 r.p.m., the torpedo boat makes a half turn in 50 sec. Find the direction and magnitude of the torque developed on the bearings of the shaft.

Problem. A certain locomotive has four pairs of drive wheels, each pair with the connecting axle having a mass of 4000 lb., a diameter of 64 in., and a radius of gyration of 20 in. Find the value of the gyroscopic couple tending to lift the wheels on one side of the locomotive when the locomotive is moving with a speed of 60 mi. per hr. around a curve of 1000-ft. radius. Neglect any inclination of the axles to the horizontal.

Solution. From (58), the gyroscopic couple

L[= Kswswl = 4 mk2 r R = 4    klv2

where m is the mass of one pair of wheels with the connecting shaft, k is the radius of gyration of the rotating system, v is the speed of the train, R is the radius of the curve, and r is the radius of each drive wheel.

L _ (4(4000) slugs) (20 ft )2 (60 X 5280 ft. per sec. /2 ( 12.   1

32.1   12   3600   / 32 ft. 1000 ft. = 4020 lb.-ft.

Problem. A steamship is propelled by three steam turbines rotating in the same direction about a fore-and-aft axis at the rate of 200 r.p.m. The moments of inertia of the three rotors together with the connected shafts and propellers are 1400, 700, and 1400 ton-foot2 units, respectively. Find the magnitude of the gyroscopic couple developed when the ship is pitching with a maximum angular speed of 0.1 radian per second.

Solution. From (58), the torque L = Kswsw. Since one revolution equals 2 a radians, the angular speed of the shafts is

WS = 2006(02 7) radians per sec.