68   MOTION OF A SPINNING BODY

Any gyroscope exhibits nutation of the spin-axle on the sudden application of a torque, but the long arm of Fessel's mounting renders the nodding especially conspicuous. The amplitude of the nutational dip depends upon the amplitude and suddenness of development of the gravity torque. Nutation would continue indefinitely if there were no opposition to the dipping due to air or bearing resistance, as for example in the case of the nutation of the earth's axis. In the case of most gyroscopes the nutation is quickly damped to zero.

Suppose that the gyro is spinning at constant rate in the clock

wise direction as seen when viewed from the counterpoise toward

the gyro. In addition, suppose that the position of the counter

poise is such that there is a torque L in the clockwise direction

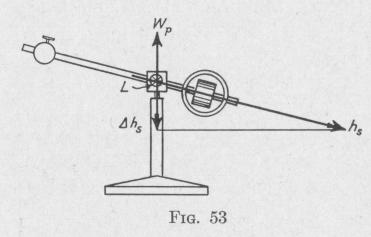
about a horizontal axis as indicated in Fig. 53. Note that there

is zero external torque about the vertical axis.

At the instant the gyro-frame is released, there is zero preces

sion and the heavy end tilts downward below the horizontal. This

tilting gives a vertical component ahs of the angular momentum h5, directed downward, Fig. 53. There must be zero torque about the vertical axis. Another angular momentum must be generated about the vertical axis at the same rate and in the direction op

posite to the vertical component of h3. This is produced by the

development of angular velocity (and angular momentum) in

the direction indicated by wp. This precessional velocity is greater

than that which would have been produced if the spin-axle. had

not been tilted so much.

The gyroscope has greater kinetic energy when precessing than when not precessing, though the total energy is constant. In order that the total energy may remain constant, the accelerated precessional velocity is accompanied by a rise of the heavy end of the gyroscope.

The inertia of the system carries the heavy end above the equilibrium position. As the potential energy is increased by the elevation of the heavy end of the gyroscope, the kinetic energy of rotation must decrease, that is, the precessional velocity must diminish.

MOTION OF A SPINNING BODY   69

When the heavy end dips, the precessional velocity increases. When the heavy end rises, the precessional velocity decreases. After a few oscillations, the spin-axle will remain at a nearly constant inclination to the vertical and the velocity of precession will remain nearly uniform. The inclination of the spin-axle from the vertical, at any instant, is called the angle of nutation.

Question. The counterpoise of Fig. 52 may be replaced by a little bucket of

sand provided with a hole in the bottom through which the sand may slowly escape. Suppose that this bucket is placed near the end of the rod so as to

considerably overbalance the gyroscope, the gyro is set spinning, the rod is held horizontal and then released. As the sand escapes, the counterpoise

will, after a time, be overcome by the weight of the gyro. Describe the sequence of changes in precession and dip of the gyro-axle.

40. The Effect of Hurrying and of Retarding the Precession of a Spinning Body. Experiment. - Attach a small mass to the inner frame of the gyroscope at the point x, Fig. 35, thereby producing a torque L as indicated. Set the gyro-wheel spinning in the direction indicated. Observe that the weighted side of the inner frame dips slightly below the center of the gyro-wheel and that the gyro-axle precesses with an angular velocity in the direction represented by wp. Push horizontally against the second gyro-frame with the rubber tip of a lead pencil so that the spin-axle is moved in the direction of its precession. Observe that the weighted side of the inner gyro-frame rises. Now push on the second frame so that the spin-axle is moved in the direction opposite its precession. Observe that the weighted side of the inner frame sinks.

In each case the spin-axle moved so as to be more nearly parallel to the axis of the new torque produced by the pushing on the second frame, and with the direction of spin in the direction of the torque. This is in accord with the Second Law of Gyrodynamics (Art. 34). When an added torque causes an increase in the precessional

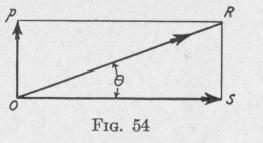
velocity, the angular momentum produced by the added torque about the precession axis is represented by the line Op, Fig. 54. This angular momentum, compounded with the angular momentum OS of the gyro-wheel about

the spin-axis, gives a resultant angular momentum represented

by OR. Thus, it appears that the spin-axis tends to precess upward through an angle 0 about an axis through 0 perpendicular to the plane of OP and OS. By a similar analysis it can he