88   MOTION OF A SPINNING BODY

contributed by the component angular velocities WA, WB and wC of the rotatable frame of reference. Since the components of the angular momentum of the spinning body about the three rotatable axes do not depend upon the position of the fixed axes, the rate of change of these quantities does not depend upon the position of the rotatable frame relative to the fixed axes of coordinates. The determination of these rates of change will be simplest when the two frames coincide.

We shall now find each of the four parts which together make up the component torque about the axis OA acting upon the spinning body. First, note that if the rotatable frame were at rest, the rate of change about the axis OA of the angular momentum of

the spinning body would be AA . Second, note that while the

component velocity wA about the axis AO rotates the angular momenta hB and he about A0, the projections of hB and he are always zero. Consequently, a constant angular velocity wA contributes zero rate of change of angular momentum about A0.

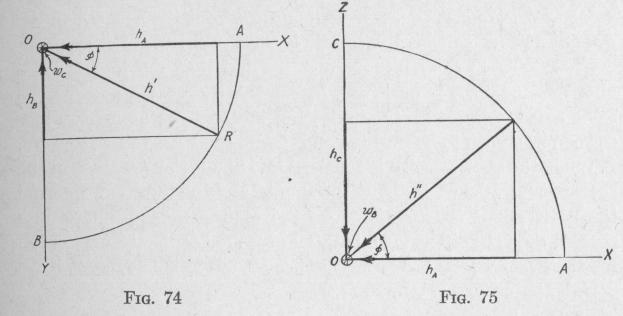
Third, consider the contribution of rate of change of angular momentum about the axis A0, due to the component angular velocity we of the movable reference frame. Imagine the component of h in the plane of AOB, Fig. 73, and represented by the line h', Fig. 74, to be rotating with angular velocity wC about an axis through 0, perpendicular to the plane X0 Y. When h' makes an angle 0 with A0, the component of h' about AO is h' cos 0. The rate of change of this component of the angular momentum relative to the axis AO is

-h'sin~ = -h'sin0•wc

When o = 0, this rate of change equals zero, that is, the rotation of hA contributes zero effect. When o = 90°, sin 0 = 1, h' = hB; that is, the rate of change of the angular momentum about the axis AO contributed by the rotation of hB equals -hBwC. This is the entire rate of change relative to OA due to wc.

Fourth, consider the rate of change of angular momentum about the axis AO, due to the component angular velocity wB of the movable reference frame. Imagine the component of h in the plane of AOC, Fig. 73, and represented by the line h", Fig. 75, to be rotating with angular velocity WB about an axis through 0, perpendicular to the plane XOZ. When h" makes an angle ¢

MOTION OF A SPINNING BODY   89

with A0, the component of h" about AO is h" cos 0. The rate of change of this component of the angular momentum relative to the axis AO is

-h" sin O do = h" sin o • wB

When 0 = 0, the rate of change equals zero, that is, the rotation of hA contributes zero effect. When o = 90°, sin 0 = 1, h" = hc; that is, the rate of change of the angular momentum about the

axis AO contributed by the rotation of he equals hCWB. This is the entire rate of change relative to OA due to WB.

Collecting the values of the four torques composing the component acting upon the given body about the axis OA, and representing this component by the symbol LA, we have,

LA = dh - 0 + hCWB - hBWC   (70)

Proceeding in the same manner, we find the component torqu acting upon the given body about the axes OB and OC to be, i spectively,

LB = d B - 0 + hAWC - hcwA   (7

Lc =

dhc

- 0 + hBWA - hAWB   (7

The signs of the last two terms of (70), (71) checked by the folio-wino, ennsiderations.