the pulverizing ring, the azimuthal plane makes one revolution in the opposite direction. Thus, the number of revolutions made by a roll of radius r while rolling once, without slipping, around the inside of a ring of radius R is

~R - 1), relative to the rotating azimuthal plane. Hence, (luring one revolution of the driving pulley, the roll makes R r r revolutions relative to the

azimuthal plane. The product of this fraction and the angular velocity of the driving pulley, relative to the pulverizing ring, equals the angular velocity of the azimuthal plane relative to the ring,

_ 23

'u'z - R r r rwp]   40 - 23165 = -223 r.p.m.

-

_ - 23.3 radians per second.

The negative sign is used to indicate that the motion of the azimuthal plane is in the direction opposite that of the driving pulley.

The value of _,'c, now will be determined. While the center of the roll is

going once around the pulverizing ring, the roll makes It ,wz revolutions rela

tive to the azimuthal plane. Hence, the angular velocity of the roll shaft relative to the azimuthal plane

-R   R   ]   40

zu's - ,• ru'a = R _ r r"1p - a0 - 23 165 = 3S8 r.p.m.

= 40.6 radians per second.

Substituting the data and values now found in (76), the magnitude of the torque acting upon the roll and shaft due to the rotations,

LB=-1331(-23.3)'0.12X0.99+12.9(40.6-23.3X0.99)

(-23.3 X0.12) = -864261b.-ft.

The force due to this torque acting on the roll perpendicular to the roll shaft

F = -86426 lb.-ft.   136-31h. wt. 6.33 ft.

The pulverizing ring is acted upon by the horizontal component of the reaction of this force

Fr = 13653 cos 6° 40' = 135171b. wt.

.1s the roll shaft is deflected from the vertical through an angle

0, there is a horizontal force pulling the roll away from the wing of the value, Fig. 79,

(880 X 6.33 + 600 X 3.33) sin B = 14216. wt. f =   6.33cos8

Consequently, the total force with which the roll pushes against the pulverizing ring is

I', - f = 13517 - 142 = 13375 lb. wt.

MOTION OF A SPINNING BODY   93

of 40 in. Find the force with which the roll presses against the pulverizing ring when the roll shaft is making 165 r.p.m.

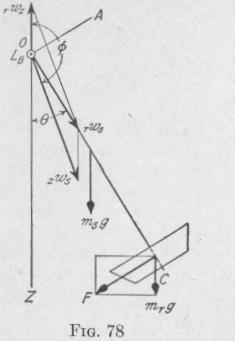
Solution. The torque acting upon the roll and shaft due to the rotation about the axis of the shaft, AC, Fig. 78, and the rotation of the axis of the shaft about a fixed vertical axis OZ, is given by

(76). Let

m, = mass of the roll = 800 lb. = 27.4 slugs

32.1

ms = mass of the shaft = 600 lb. = 18.7 slugs

32.1

l, = length of roll = 0.66 ft.

is = length of shaft = 6 ft.

d, = diameter of roll = 1.9 ft.

ds = diameter of shaft = 0.48 ft.

KA = moment of inertia of the shaft and roll

about an axis, OA, coinciding with the

diameter of one end, (25) and (27),

=ms(d2+32)+ntr(16+32+36)

= 1222 slug-ft.'

Kc = moment of inertia of the shaft and roll about the axis of the shaft, OC, (22),

= e msds2 + e mrdr2 = e (rnsds2 -{- m,d,2)

= e (18.7 X 0.23 + 27.4 X 3.6) = 12.9 Slug -ft.2

9 = deflection of the roll shaft from the vertical = sin-,(1.66 - 6 0.95)

= 6° 40'.

r'wz = angular velocity, about a vertical axis, of the azimuth plane through

the roll shaft and the point of suspension, relative to the pulverizing

ring. In (76) this is represented by wz.

zws = angular velocity of the roll shaft relative to the rotating azimuth

plane. In (76) this is represented by ws.

rws = angular velocity of the roll shaft about its axis, relative to the pul

verizing ring

= b05 2 rr = 17.2 radians per second.

The values of rw, and zws now will be determined. The number of revolu

tions made about the axis of the roll shaft by a roll of radius r while rolling

once, without slipping, against the inside of a ring of radius R is

n=R-1

r

Therefore,

rwz[ = -,n s] _ - R `wsr = -23 radians per sec.   (78) The negative sign is used to indicate that rwz is in the sense opposite that of rws.