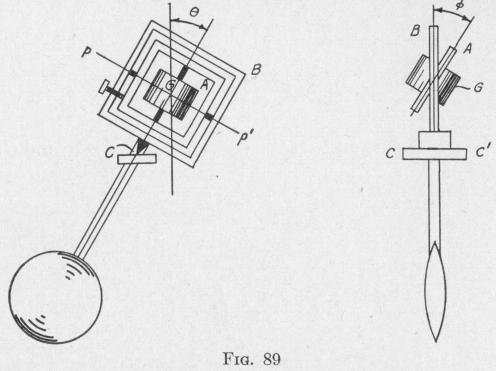
112   THE GYROSCOPIC PENDULUM

If the outer frame be turned through a small angle 0 with angular velocity d~ about an axis at C normal to the plane of the frames

while the gyro-wheel is spinning and the two frames are clamped together, the inner frame will be acted upon by a torque about the

axis pp' equal to Kw, dO

If the two frames are not clamped together, the inner frame will precess through an angle 4 in time t, about the axis pp', with an

2

angular acceleration d0. If 0 remains small, we have from (19)

and (58)

z

Kp d o = Ksws dl

where Kp is the moment of inertia of the inner frame together with the gyro-wheel, with respect to the axis pp' about which the inner frame is turning.

Let us measure angles and time from the instant when the two frames are in the same plane. At this instant t = 0 and 0 = 0. Integrating the above expression between the limits 0 and t, we have, when 0 is small,

Kph = Ksw,0+0
or   d __ Ksw.,O   (89)

fit.   K.

GENERAL PROPERTIES   113

If the inner frame were clamped so that the gyro could no precess, a certain torque would be required to give the apparatu a chosen angular acceleration. When the gyro is precessing, th( centrifugal couple must be balanced by an additional torque In order to give the apparatus the chosen angular acceleration it ii necessary to apply an outside torque which is the sum of these tw( components. That is,

2

L, = K, d20 + Ksws do

Substituting in this equation the value of ,0-, found aboi

L, = K6 20+K,2 s20   (90

p

This is the torque about an axis normal to the precession axis that is required to turn the inner frame together with the gyro-wheel with an angular acceleration.

When the inner frame with the gyro-wheel is turned with constant velocity, the first term in the right-hand member of the above equation is zero. Consequently, when the gyro-axle of a precessing gyro-wheel is turned with constant angular velocity through a small angle 0 about an axis perpendicular to the precession axis, the precessing wheel exerts a torque on the restraints of the value

Lc' = Ks2ws20 = hs20   (91) Kp Kp

where Kp is the moment of inertia of the gyroscope with respect to the precession axis.

70. The Length of the Simple Pendulum That Has the Same Period as an Oscillating Body to Which is Attached a Spinning Gyroscope. - When the gyroscope is not spinning, the pendulous body has a period given by (50). A simple pendulum has a period given by (51). If the simple pendulum has the same period as the pendulous body,

K, k2

l mH H   (92)

where H represents the distance from the center of mass of the pendulous body to the knife-edge, m is the mass of the pendulous body, K, is the moment of inertia of the pendulous body with respect to the axis of oscillation, and 1 is the length of the simple pendulum that has the same period as the given pendulous hndv.