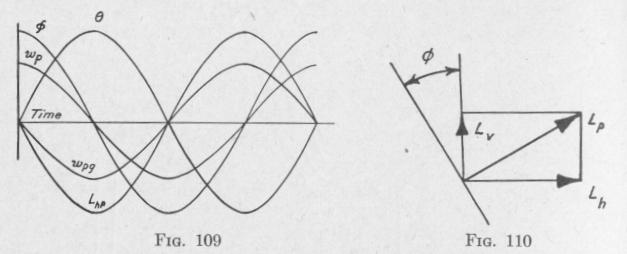138   ANTI-ROLL DEVICES FOR SHIPS

acting on the pendulum is maximum and consequently the deflecting torque on the pendulum is maximum.

The swinging of the pendulum and the precession of the gyro-axle have a common period. When the velocity of precession is maximum, the angle of precession 0 is zero, Figs. 107 and 108. Consequently, when the deflection 0 of the pendulum from the vertical is maximum, ¢ is zero. The variation of 0 with respect to time is represented by the curve marked 0 in Fig. 109. The variation of 0 with respect to time is represented to a fair degree of accuracy by the curve marked ¢.

The angular velocity of the pendulum due to gravity is zero when the inclination of the pendulum to the vertical is maximum, and the velocity is maximum when the inclination is zero. The relation between the angular velocity of the pendulum and time is represented approximately by the curve marked wp.

At the instant when the pendulum is at the end of a swing, 0 is maximum, the gyro-axle is passing through its mid-position (4, = 0), the speed of precession wpg is maximum, and the torque LP acting on the pendulum due to the attached gyroscope is maximum.

When the angle between the gyro-axle and the vertical is 0, Fig. 108, there is a vertical component of the torque acting on the pendulum due to the precession of the attached gyroscope of the value, Fig. 110.

Lv = LP sin ¢ = hswpg sin 4,

This vertical component tends to twist the pendulum about the axis of the pendulum, as was observed in the experiment. The component about a horizontal axis parallel to the knife-edge is

L.P = L, cos 6 = h.w ens th

THE INACTIVE TYPE OF GYRO SHIP STABILIZER 139

The variation of Lhp with respect to time is represented with a certain degree of precision by the curve marked Lhp, Fig. 109.

The power imparted to the pendulum by the gyroscope at any instant equals the product of the torque acting on the pendulum at that instant due to the gyroscope Lhp and the angular velocity of the pendulum, wp. The average value of the power during one complete vibration is given by a curve of products of the instantaneous values of LhP and wp. It will be observed that the curves of LhP and wp are in quadrature, that is, they differ in phase by 90 degrees or a quarter of a period. Now the average value of the product of two sine curves of the same frequency is zero when the curves are in quadrature (Art. 25). That is, if the relation between LhP and time, and that between wp and time, were accurately represented by sine curves in quadrature, then the average power applied to the pendulum throughout one vibration by the precessing gyroscope would be zero. Consequently, under the conditions specified, the vibrations of the pendulum are undamped.

If, however, the phase difference between the LhP curve and the wp curve were greater than 90 degrees, then the power imparted to the pendulum by the precessing gyroscope would be negative, that is, energy would be abstracted from the pendulum. The more nearly the two curves are to being in opposite phase the greater will be the damping. They may be brought more nearly into this condition by retarding the Lhp curve relative to the wp curve. This can be done by opposing the motion of precession wpg by a friction brake. Friction at the bearings AA', Fig. 107, constitutes a torque about that axis in the direction opposite the precession. This torque produces a precession of the inner gyro-frame about an axis perpendicular to the plane of the diagram which opposes the velocity of the pendulum and increases the phase difference between Lhp and wp. The power absorbed from the pendulum is now no longer zero. The vibrations of the pendulum are damped. The amplitude of vibration of the pendulum would not be damped if there were no opposition to the precession of the gyro.

The method here indicated for bringing variations of the precessional velocities of the gyro-axle of a spinning gyroscope more nearly into opposite phase with the variations of the torques acting on an oscillating body that carries the gyroscope is the basis of the action of the ship stabilizers of the inactive type designed by Schlick, Fieux. and others.