174   NAVIGATIONAL COMPASSES

required precession can be produced by a torque about a horizontal axis which tilts the gyro-axle from the horizontal plane. Two different methods are now in use to produce this tilting torque on the spin-axles of gyro-compasses. One is by making the sensitive element pendulous. In the following Article the other method will be considered in which the tilting torque is produced by a moving mass of liquid.

Now it will be shown how the weight of a mass attached to the
supporting frame of a spinning gyro-wheel below the center of the
gyro-wheel, will cause the spin-axle to precess toward the me

ing frame of a gyro-wheel "a pendulous mass." The pendulous
mass will be pulled toward the center of the earth. This pull will
produce zero torque when the gyro-axle is horizontal as at X.
While the earth rotates, the spin-axle of the gyro-wheel tends to
maintain its position in space with the result that, when the gyro
scope has reached a position Y, the axle is no longer horizontal.
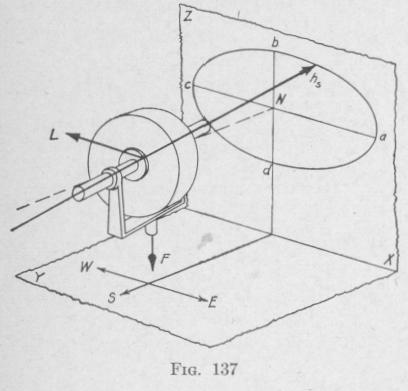
The weight F of the pendulous mass exerts a torque in the counter
clockwise direction about an axis perpendicular to the plane of the
diagram. The line L, representing the torque, is directed upward
from the plane of the diagram. Suppose that the direction of spin
is as represented by the line hs. Then, from the law of precession,
the spin-axle tends to become parallel to the torque-axis with the
direction of spin in the direction of the torque. In the present
case, the direction of the torque is the same as the direction of
rotation of the earth. Therefore, the gyro-axle of the pendulous
gyroscope tends to become parallel to the earth's axis, with the

THE VARIOUS TYPES   175

direction of spin in the same direction as the rotation of the earth. In the same manner it can be shown that if the center of mass of the gyroscope is above the point of support, the gyro-axle tends to become parallel to the earth's axis, with the spin in the opposite direction to the rotation of the earth.

When the spin-axle reaches the meridian plane (position Z, Fig. 136), the north-seeking end of the gyro-axle is at its maximum elevation above the horizon and the weight of the pendulous mass is exerting its maximum torque thereby producing a maximum velocity of precession. The gyro-axle will cross the meridian

plane and, continuing its angular motion beyond the meridian plane, the axle will dip and pass through the horizontal position. During the dipping, the torque due to the weight of the pendulous mass decreases till it is zero when the spin-axle is horizontal. At this instant, the precessional velocity is zero and the spin-axle is at its greatest angular displacement from its original direction at X. Continuing its dipping, the north-seeking end of the spinaxle passes through the horizontal plane, raising the pendulous mass and thereby developing a torque in the opposite direction. The north-seeking end of the spin-axle rises, again crosses the meridian plane and repeats its motion back and forth. The oscillation of the spin-axle of a gyro-compass back and forth through the meridian plane involves an exchange of energy between the compass and the earth.

It has now been shown that the deflection of the spin-axle of a