186   NAVIGATIONAL COMPASSES

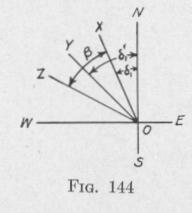
ZO. The ballistic deflection is XOZ. The angle YOZ by which the gyro-axle either overshoots or undershoots the correct settling position for the particular latitude, course and speed, is called the ballistic deflection error. With any change in the meridian component of the ship's velocity, the spin-axle will be deflected in the same direction as the movement of the gyro-axle produced by the change in the meridian-steaming error. When the acceleration of

the ship's velocity ceases, the gyro-axle oscillates about the resting position YO. There will be zero ballistic deflection error if XOZ = XO Y, that is, if the ballistic deflection equals the change in the meridian-steaming error.

In order that the compass card may be in its true resting position throughout the time the velocity of the ship is changing, the com

pass must be forcibly precessed, during this time, to the resting position proper to the speed, course and latitude at the end of the acceleration.

If the gyro were not spinning, the spin-axle would tilt throughout the time the velocity of the ship is accelerating. If, however, the gyro were spinning, the " rigidity of plane " would oppose tilting. In this case, the pendulous mass would be acted upon by a force which would develop precession about a vertical axis. If the precessional velocity were of the proper magnitude, it would cause the compass to precess, during the time the velocity of the ship is accelerating, from the resting position proper to the speed, course and latitude at the beginning of acceleration, to the resting position proper to the speed, course and latitude at the end of the acceleration. Under this condition, there would be zero ballistic deflection error.

113. The Period of a Gyro-Compass That Will Have Zero Ballistic Deflection Error When at a Definite Latitude. - The magnitude of the ballistic deflection depends upon the torque that opposes tilting of the sensitive element. In the case of a gyrocompass of the pendulous type at a given latitude, the torque that opposes tilting depends upon the degree of pendulousness of the sensitive element. In the case of a liquid-controlled non-pendulous gyro-compass at a given latitude, it depends upon the weight of liquid that is moved from one side of the gyro-case to the other and upon the distance between the opposite mercury reservoirs. Each

NATURAL ERRORS   187

of these factors affects the period of vibration of the spin-axle back and forth through the meridian. It will now be proved that if the period of the sensitive element has a certain value, which for all latitudes is not far from 84 minutes, then the spin-axis of the gyro-compass will move, without oscillation, to the resting position appropriate to the given speed and course, just as soon as any change occurs in either the speed or course.

Imagine a symmetrical body supported at the center of mass so as to be capable of turning about this point in any direction. An

acceleration of the motion of the body in any direction will produce no turning of the body.

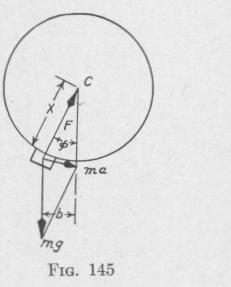
Imagine, farther, that a mass m be attached

to the body at a distance x from the center of mass C, Fig. 145. When the motion of the system is constant, the mass m is acted upon by a force mg vertically downward and by an equal force vertically upward. If the linear motion of the system is subject to a constant acceleration a in a horizontal direction to the right, the pendulous part m of the system must be acted upon by a force ma in the direction of

the acceleration. This force is the resultant of the weight me vertically downward and a force F directed toward the point C This force F is inclined to the vertical at an angle 0, given by thi

relation

When the horizontal distance of m from the vertical line through C is b, the system is acted upon by a torque about an axis perpendicular to the plane of the diagram of the magnitude

L = mgb = mgx sin ¢

When 0 is so small that sin ¢ may be replaced by tan 0, we have, on substituting the value of sin 4> from the above equation, in

(120):

L = mxa

Suppose that the suspended system includes a gyro spinning about a nearly horizontal axis. We are now dealing with a pendulous gyro-compass. If the ship carrying the gyro-compass be accelerated while on a meridian course, the pendulous part of the