20 PRINCIPLES OF ELEMENTARY DYNAMICS
torque. It is producing angular momentum about its own axis perpendicular to the plane containing h and the axis of the rod. This angular momentum, combining with the h of the previous position of the rod, gives the h in the new position. We have here an example of the case in which the axis of the resultant angular momentum does not coincide with the axis of the resultant angular velocity.
16. Conservation of Angular Momentum. - In the special case in which a rigid body is acted upon by a system of torques the sum of which, relative to a given axis, is zero, we have (28):
L _ Kdw=0
dt
That is, in this special case, the time-rate of change of angular momentum is zero. In other words, the angular momentum is constant. Therefore, if a rigid body is acted upon by a set of external torques, the resultant of which about any assigned axis fixed in space is zero, the angular momentum of the body relative to the assigned axis is a constant quantity. From this equation it follows that:
However the parts of any material system may act upon one another, the total angular momentum of the system, about any axis fixed in space, will remain constant, so long as the system is acted upon by no outside torque. This theorem is called the Principle of the Conservation of Angular Momentum.
If a circus performer wishes to turn a series of aerial somersaults, he will jump from a springboard in such a way that he will give himself a considerable angular velocity about a horizontal axis. While turning the first somersault he will hold his body nearly straight, but after that he will gradually draw his head and knees together, thereby decreasing the moment of inertia of his body about the axis of rotation. Since the angular momentum of his body remains constant, when the moment of inertia is diminished the angular velocity of his body is increased to such an extent that he can make more somersaults before reaching the ground. If, when he has nearly reached the ground, he sees that he will fall face downward, he will straighten his body, thereby increasing his moment of inertia, thus decreasing his angular velocity to such an extent that he can alight on his feet.
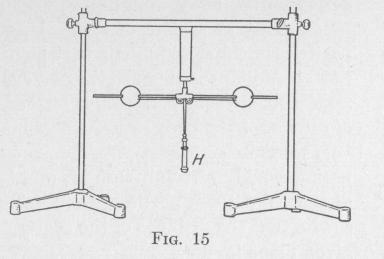
Experiment. - Set into rotation about a vertical axis the horizontal rods carrying the two metal spheres, Fig. 15. Pull on the
TRANSLATION AND ROTATION 21
handle H, thereby drawing the spheres close to the axis of rotation and diminishing the moment of inertia of the rotating system. Note that the angular velocity of the system is now much greater
than before. Release the
pull on the handle. The spheres retreat from the axis of rotation, thereby increasing the moment of inertia of the rotating system. Note that the angular velocity diminishes. During these operations no torque was applied to the rotating body about the
axis of rotation. Consequently, there was no change in the angular momentum of the system.
Although the work done in pulling the spheres toward the axis of rotation does not change the angular momentum (Kw) of the rotating system, it does increase the kinetic energy of rotation (2 Kw2) of the system. While approaching the axis of rotation, the spheres are moving not in a circular path but in a spiral path. The force in the string is not perpendicular to the path. There is a component of this force that acts upon the spheres in the direction of the tangent. This tangential component of the force produces an increase in the tangential velocity and also in the angular velocity.
17. Centroid, Center of Gravity and Center of Mass. - The point of application of the resultant of a system of parallel forces is called the centroid or center of the system of forces.
" If the action of terrestrial or other gravity on a rigid body is reducible to a single force in a line passing always through one point fixed relatively to the body, whatever be its position relative to the earth or other attracting mass, that point is called the center of gravity."* The only bodies which have true centers of gravity are uniform spherical shells, uniform spheres, and spheres whose density changes from the center to the circumference according to some definite law. In the case of other bodies, the line of action of the weight of the body does not pass through the same point when the position of the body is changed. In engineering, however, it is customary to assume that there is a definite point
* Thompson and Tait, Natural Philosophy, II, p. 78.