30 PRINCIPLES OF ELEMENTARY DYNAMICS
support will sweep out a conical surface. The body will move around and around with a definite period. A suspended body which, owing to its weight, is capable of rotating in such a manner that the line through the point of suspension and the center of mass has constant angular velocity about the vertical line through the point of suspension is called a conical pendulum.
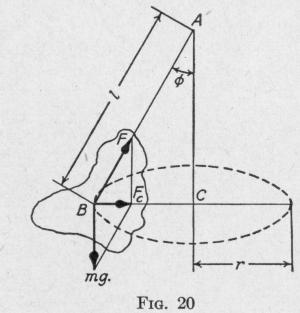
An expression for the period of a conical pendulum now is to be determined. In Fig. 20, a body of mass m with center of mass at
B is supported without friction at
A. When set into motion, the body rotates so that the center of mass traces a circle of radius r about a center C vertically below the point of suspension A.
The resultant force acting on the body is the centripetal force directed toward the center of the circle. This is due to the weight mg of the body, and the reaction F of the support. Representing the distance AB by 1, the angle
BAC by A, the linear speed of the
center of mass in the horizontal circle by v, and the period of a
revolution by T, the value of the centripetal force is
12
Fr = [F sin ~] = mv2 r = r m (2 rr''T
Also,
F cos cb = mg
Dividing each member of the former equation by the corresponding member of the latter, we have:
sin 0 4 r2r _ 4 r2 l sin cos 0 T2g T29
Whence, the period
T = 21rV o (52)
23. Wave Motions and Wave Forms. - A motion that goes through the same series of changes at regularly recurring intervals is called periodic. A periodic disturbance which is handed on
SIMPLE HARMONIC MOTION
successively from one portion of a medium to another is called a wave motion.
It is convenient to represent graphically a periodic function by a curve coordinating the function and time. Thus, if we plot instantaneous values of the electromotive force in an alternating current circuit against time, we obtain what is called the wave form of the periodic alternating current. If we plot a ship's instantaneous angle of roll against time we obtain the wave form of the roll. If the quantity varies as the sine or the cosine of an angle, then the wave form is called a sine curve, or a cosine curve, respectively. Either a sine curve or a cosine curve is a harmonic curve or harmonic wave form.
The value of the angular displacement from the equilibrium position of a body vibrating with simple harmonic motion of rotation is given by (48), where T is the period of the vibration, 4>
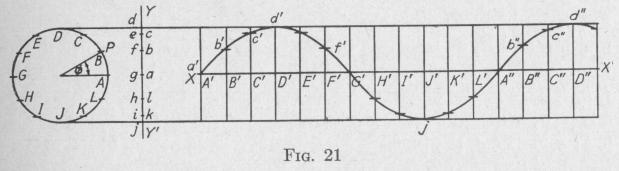
is the amplitude, and 0 is the angular displacement from the equilibrium position at time t. The angular displacements made in succeeding equal time intervals are proportional to the distances ab, bc, cd, de, ef, fg, etc., Fig. 21. To obtain these unequal distances, project onto the line YY' the positions at the end of equal time intervals of a point P moving with uniform speed in the circumference of a circle (Art. 18). In the case here represented, the circle, Fig. 21, is divided into twelve equal arcs, AB, BC, CD, etc. On, the line XX' mark thirteen points A', B', C', etc., at equal distances apart. Through each of these points draw a line perpendicular to XX'. Draw a line parallel to XX' from each of the points marked on the line YY'. Place a dot a' at the intersection of the horizontal line through a and the vertical line through A'. Similarly, place a dot b' at the intersection of the horizontal line through b and the vertical line through B', and so on for the remainder of the intersections c', d', etc. The smooth curve drawn through these dots is the wave form of the simple harmonic motion represented by (48). The period T is the time required to