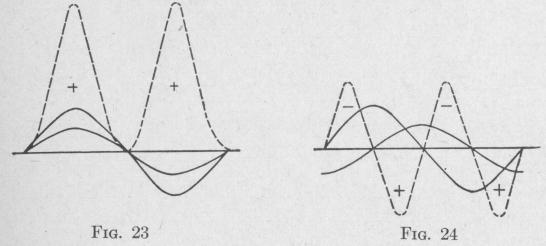34   PRINCIPLES OF ELEMENTARY DYNAMICS

forms of the two vibrations are sine curves as shown. The product of the two functions at any particular instant is*

'd,d2 = rlr2 sin 0 sin (0 + i3) = r2 2 [cos Q - cos (2 0 + j3)] (53) Since

20+$=2(2Tt)+R

it follows that during one-half cycle, that is, while t changes to t + 12 T, and 0 becomes (0 + ir), the angle (2 0 + 3) becomes

2 (2lrt +7) + 0. Whence, the change of argument of the last

cosine in (53) is 2 it radians. The argument of the cosine is a linear function of time. During this change of angle, the cosine goes through all values, positive and negative, and the mean value of. cos (2 0 + 3) during any half period is zero. Consequently, the mean value of the product of two simple harmonic functions of equal period and of amplitudes r1 and r2 is

d,d2 = z r1r2 cos 0   (54)

where 0 is the difference in phase of the two functions.

For example, if the two harmonically varying quantities d, and d2 represent instantaneous values of electric current and electromotive force, respectively, then the power of an alternating current during any half period is given by (54), where r, and r2 represent the maximum values of the current and electromotive force, respectively, during the half period, and 03 represents the difference of phase between current and electromotive force. Or, if the two quantities d, and d2 represent instantaneous values of angular speed and torque, respectively, then the power transmitted to the oscillating body during any integral number of half periods is given by (54) where r, and r2 represent the maximum values of the angular speed and torque, respectively, and 0 represents the difference of phase between angular speed and torque.

Equation (54) shows that:

(a) When two harmonic functions, d1 and d2, of equal period are in the same phase, that is, when a = 0, the mean value of the product d1d2 is maximum and equals one-half of the product of the amplitudes of the two components.

* From the trigonometric relation:

sin x sin y = z [cos (x - y) - cos (x + y)]

SIMPLE HARMONIC MOTION   35 (b) When the two components are in quadrature, that is, when the phase difference i3 equals 90° or C'lr radians, the meal

the product d,d2 equals zero.

(c) When Q = it radians or 180°, the mean value of the product d,d2 equals one-half of the product of the amplitudes of the two components but with the negative sign.

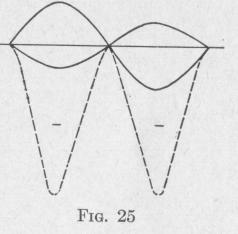
These three cases are represented graphically in Figs. 23, 24 and

25, respectively. In each figure, the harmonic curves shown in full lines represent the equations

d, = r, sin 2Tt

and   d2 = r2 sin (2lrt + a)

where a is the difference in phase. In Fig. 23, the difference in phase a = 0; in Fig. 24, 0 = 2 radians or 90°; in Fig. 25, p = 7r

radians or 180°. In each figure, the or

dinate of the dashed curve corresponding to any particular instant equals the product of the ordinates of the two harmonic curves at that instant. Thus, the dashed curves represent the variation of the product, at every instant, of d, and d2. In case d1 and d2 represent either electromotive force and current or torque and angular

velocity, then the product is power. The dashed curve then shows the variation of power with respect to time. The area between