60   MOTION OF A SPINNING BODY

(c) The weight of the larger engine is Lg _ Ksg wsw4 __ Lg

mg k2 k2 k2w,wp

(150 X 151b.-ft.)32.1 ft. per sec. per sec.   = 355 lb. wt. =    14   2

(12ft.1 136 red, per sec. (1.1 rod. per sec.)

Problem. The mass of a certain motorcycle is 350 lb., and the distance between wheel axles is 5 ft. Each wheel has a mass of 15 lb., diameter of 26 in., and radius of gyration of 12 in. There is a flywheel of 45 lb., and radius of gyration 5 in., with spin-axis in the direction of travel. The flywheel makes 3400 r.p.m. when the motorcycle is traveling 60 mi. per hr. The rider weighs 170 lb.

Neglecting the effect of any inclination of the machine from the vertical, and assuming that when the machine is at rest the wheels exert equal forces against the ground, find: (a) the gyroscopic torque tending to overturn the machine when making a curve of 300-ft. radius; (b) the vertical components of the reactions of the wheels against the ground at the same time.

Ans. (a) 22.3 lb.-ft.; (b) 255 and 265 lb. wt.

36. The Direction and Magnitude of the Torque Developed by a Spinning Body when Rotating About an Axis Perpendicular to

the Spin-Axle. - Consider a gyro-wheel with axle vertical and

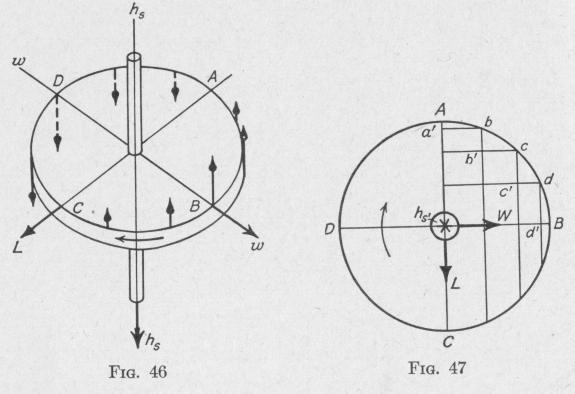
angular momentum h, in the direction indicated in Fig. 46. Suppose that the gyro-axle is rotating with angular velocity w in the direction indicated. While the wheel is rotating, the particle at A is raised, the particle at C is lowered, while the particles along

MOTION OF A SPINNING BODY   61

the axis of rotation of w are unaffected by the rotation about that axis. All particles of the wheel are moving about the spin-axis h,. While a particle of the wheel moves from the point in space A to the point B, the component linear velocity of the particle changes in the direction of the spin-axis from a finite value to zero. Suppose that the points A, b, c, d, B, Fig. 47, are the positions of a particle after moving for equal intervals of time with constant speed about the spin-axle perpendicular to the plane of the diagram. If the plane of the wheel is at the same time rotating about an axis DB, the change in the magnitude of the linear velocity in the direction perpendicular to the plane of the wheel of a particle while moving from A to b is represented by Aa', and the changes while moving during succeeding equal intervals of time are represented by bb', cc', dd'. The rate of change of linear velocity increases as the particle moves from A to B. The inertia of the particle causes it to oppose this change of velocity by a force proportional to the rate of change of linear velocity of the particle. The forces exerted by the particle when at various points between A and B in opposition to the change of linear velocity normal to the plane of the wheel, are represented by arrows in Fig. 46.

While moving from B to C, the component of the velocity of the particle normal to the plane of the wheel increases from zero at B to a maximum at C. During the displacement from B to C, the inertia of the particle causes it to oppose this change of velocity at each point of its path by a force which is in the direction opposite to the velocity normal to the plane of the wheel. In Fig. 46, the forces at different points from B to C are represented by arrows. It is thus seen that each particle in the half of the wheel ABC tends to rise, thereby producing a rotation of the wheel about the torque-axis L. In a similar manner it can be shown that the half of the wheel CDA tends to rotate downward about the same axis.

Therefore, when the axle of a' spinning body is rotating about an axis perpendicular to the spin-axis, a torque is developed on the body about an axis perpendicular to the plane of the spin-axis and the axis of rotation. The direction of this internal torque is opposite that of the external torque which would need to be applied about the same axis in order to produce a precession of the gyro-axle in the direction in which the gyro-axis is rotating.

The reaction of this torque acts in the opposite direction about the same axis on the agent that causes the rotation of the spin-axle.

When a torque is applied to an unspinning gyro about an axis