64 MOTION OF A SPINNING BODY
Whence, the torque developed by the pitching is
L[= Kswsw] = 2000 1400 + 700 + 1400 slug-ft., f (400 n rod .\ \01 rod.)
32.1 / l 60 sec.') sec J
= 2000(228) lb.-ft. = 228 ton-ft.
Problem. A certain passenger locomotive has a mass m = 293,000 lb.; distance of the center of mass from the plane of the rails b = 7 ft.; each of the four pilot wheels has a radius ri = 20 in.; each of the six drivers has a radius r2 = 40 in.; each of the two trailer wheels has a radius r3 = 26 in.; each pair of pilot wheels with the connecting axle has a mass mi = 2100 lb.; each pair of drivers with the connecting axle has a mass m2 = 8000 lb.; the two trailers with the connecting axle have a mass m3 = 2700 lb.; the radius of gyration of each pair of wheels with the connecting axle is 0.7 of the radius of the wheels. The distance between the centers of the rails, i = 56.5 in. = 4.71 ft.
Assuming that the locomotive is moving around a curve of radius R = 2000 ft., superelevated at an angle 0 = 4°, with a speed of 60 mi. per hr., find: (a) the centripetal torque, with respect to an axis parallel to the rails and midway between them, which tends to overturn the locomotive; (b) the gyroscopic torque, with respect to the same axis, due to the rotating wheels, which tends to overturn the locomotive; (c) the gravitational torque, with respect to the same axis, that opposes overturning. (d) With the locomotive running at the same speed along a straight level roadway, find the direction and magnitude of the gyroscopic torque developed when the wheels on one side pass over a high section of rail 1000 ft. long with a maximum elevation 0.1 ft. high at the middle, the other rail being horizontal.
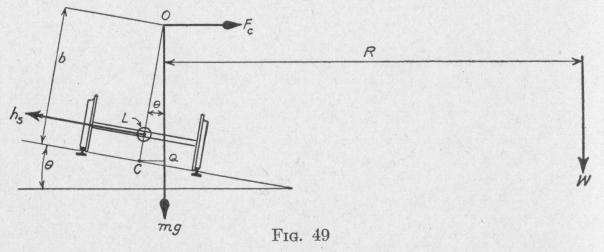
Solution. Figure 49 represents a locomotive moving away from the observer and making a right-hand curve.
(a) In order that the locomotive may move around the curve, there must be a force acting at the center of mass directed horizontally toward the center of the curve of the magnitude
mv2
F` R
Consequently, there must be a centripetal torque having a magnitude with respect to an axis perpendicular to the plane of the diagram through C, Fig. 49,
L2[= F,(OQ)] = R2 b cos 0 (60)
MOTION OF A SPINNING BODY 65
If this torque be not applied, the locomotive tends to overturn, rotating away from the center of the curve about a horizontal axis perpendicular to the plane of the diagram. Substituting in (60) the data of the problem, we find the value of the centripetal torque tending to overturn the locomotive to be
L, = 293,000 slugs (88 ft. per sec.)27 ft. (0.998) = 246,600 lb.-ft. 32.1 2000 ft.
(b) In order that a rotating axle may be turned about a vertical axis, it must be acted upon by a gyroscopic torque toward the center of the curve, about a horizontal axis perpendicular to the axle. The reaction of this torque acts upon the locomotive in the opposite direction (Art. 36).
The value of this torque acting on the locomotive, due to all six pairs of wheels, is
L2 = (2 hs + 3 he" + hs"') w cos o (61)
where hs' represents the angular momentum of each of the pairs of pilot wheels with connecting axle, and h2" and hs'" represent the angular momenta of the drivers and trailers, respectively.
From the data of the problem:
= v 2100 0.7(20) ft.) 188 ft. per sec. _
hs = KS ws - ms k12( r, = 32.1 slugs 12 ) 20 - 4701
12 ft.
Similarly, we find that
hs" = 35858 and h,"' = 7858 per sec W cos 8 = R cos of = 88 ft 2000 ft. 0.998
= 0.044 radian per sec. Hence the magnitude of the gyroscopic torque is
L = [2(4701) + 3(35858) + 7858]0.044 = 5493 lb.-ft.
(c) The gravitational torque about a horizontal axis parallel to the rails is clockwise and has the magnitude
L3 = mgb sin 0
= 293000 lb. wt. (7 ft.)0.07 = 143,570 lb.-ft. (62)
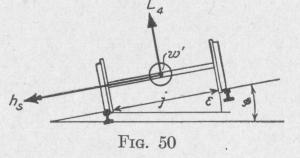
(d) When one side of the locomotive ascends a high spot, the axles rotate about a horizontal axis parallel to the straight rail with angular velocity w', of the magnitude, Fig. 50:
w' _ 0 = t radians per sec.
The linear velocity of the train while ascending the elevation, Fig. 51, v = I ft. per sec.
so that w' = eV radians per sec.
j
Consequently, when the wheel on one end of an axle ascends an elevated spot, there is developed a gyroscopic torque about an axis perpendicular to the plane