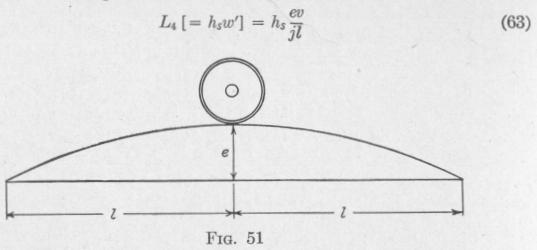
66 MOTION OF A SPINNING BODY
of the axis of w' and of the spin-velocity w,. The direction of this torque about its axis is opposite that of the torque which would need to be applied about the same axis in order to produce a precession of the axle in the direction of w'. This torque urges the ascending wheel in advance of the wheel on the level rail. The magnitude of this gyroscopic torque due to a single pair of wheels with connecting axle is
The torque developed by the six wheels on one side of the locomotive ascending the bump is
EL,=[2h3'+3hs"+hs"']fit
_ [2(4701) + 3(35858) + 7858] 01(88) = 462 lb.-ft. 4.71(500)
On descending the bump an equal torque is produced in the opposite direction about the same axis. These torques tend to spread the rails.
37. The Period of Precession. - The period of precession, that is the time T required by the spin-axle to make one complete revolution with constant angular velocity wp about the axis of precession, is given by the expression
B[= Twp] = 27r radians
When the spin-axle and the precessional axis are perpendicular to one another, the maintenance of the precessional velocity requires a torque about an axis perpendicular to the spin-axle and the precession axis of the value, (55), L = Kswswp. Consequently,
T P 27r]_ 2 rrKsws _ 2 irh, (64)
-WP]- L L
38. The Kinetic Energy of a Precessing Body. - The kinetic energy of a gyro-wheel of moment of inertia K, spinning with an
angular velocity ws is z Ksws2, (11). So long as ws remains con
stant, the kinetic energy due to spinning is constant, whether there is precession or not. If a mass m be applied to one end of the spin
MOTION OF A SPINNING BODY 67
axle of the gyroscope, the spin-axle will dip through an angle 0, and a torque L, will be developed about the torque-axis. The spin-axle will precess about an axis perpendicular to the spin-axle and the torque-axis.
A torque imparts kinetic energy of rotation to a body only when the torque produces angular velocity about the torque-axis. Consequently, the torque L, imparts kinetic energy to the spinning body only in producing the dip 0. Hence, the kinetic energy of precession equals the work done by the torque L, in producing the dip 0 and has a value equal to L,o. Therefore, the total kinetic energy of the precessing body is
W,o = a Ksws2 + Lt¢ (65)
The spin-velocity ws of a gyro-wheel is not altered by the application of a torque that produces a precession of the gyro-axle.
In uniform precessional motion, torque produces angular momentum about the axis of precession but does no work about that axis. This is analogous to the case of uniform circular motion in which centripetal force produces linear momentum but does no work in the direction of the linear momentum.
39. Nutation. Experiment. - Figure 52 represents a gyroscope mounted as used by Fessel. By setting the counterpoise at different places on the rod, torques about a horizontal axis can be pro
duced of different magni
tudes in either the clockwise or the counter-clockwisedirection. By means of the counterpoise, balance the gyroscope so that the rod remains horizontal. Set the gyro-wheel spinning. Observe the result.
Stop the spinning. Move the counterpoise till it overbalances the gyro. Set the gyro spinning. Hold the rod horizontal and then release. Observe that the end dips and rises and at the same time precesses with ununiform velocity. The nodding of the spinaxle is called nutation.
Stop the spinning. Move the counterpoise till it is overbalanced by the gyro. Set the gyro spinning. Hold the rod horizontal and then release. Observe the result.