TRANSLATION AND ROTATION
garded as moving and what object is taken as the reference body, it is convenient to use two subscripts. Let a subscript written at the right indicate the moving body, and a subscript written at the left indicate the frame of reference. Thus, the velocity of a for
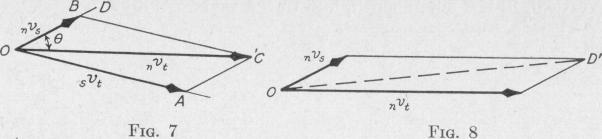
pedo with reference to the ship from which it is projected may be written 3vt, and the velocity of the ship with reference to the enemy maybe written ,,
,,. In Fig. 7, OA represents viand OB represents nvs. We notice that in these symbols for the velocities which we have compounded, the right subscript of one velocity is the same as the left subscript of the other, and that the resultant has the two subscripts that are different. In our example, svi and nvs combined give the velocity of the torpedo with respect to the enemy, nvt.
If we have given ,vt and nvs and wish svt we need only notice that nvs = -sv,,. Thus, we can compound ,,v, and -,vn thereby obtaining svt.
The " torpedo director " consists of two rods variable in length and direction which are linked together and to a third rod carrying a telescope. The telescope points in the direction vi when the other two rods are adjusted to represent in direction and length sit and nvs. When the enemy ship arrives at C, Fig. 7, it is seen in the telescope fastened to the rod OC. At this instant the torpedo is launched in the direction and with the speed relative to the firing ship represented by OA. The torpedo meets the enemy ship at A.
If, however, we attempt to combine in this manner two velocities which do not have a right subscript of one the same as a left subscript of the other, we shall have a result which is without meaning. For example, if we attempt to combine the velocity of the torpedo with respect to the enemy and the velocity of the firing ship with respect to the enemy, we would get the line OD', Fig. 8. This line has no physical meaning.
Problem. Waves are moving across the sea with a velocity of one knot westward, relative to the earth. The distance between the crests is 50 ft.
Find the number of wave crests that in one hour pass under a ship which is steaming at a velocity of 15 knots: (a) north-east; (b) south-west.
Ans. (a) 1909 crests; (b) 1739 crests.
Problem. An airplane has a supply of gasoline sufficient for six hours of flying at a speed of 60 knots relative to the air. The wind has a velocity of 15 knots from the south. The pilot is ordered to proceed as far as possible along a north-east course and then retrace his course to the starting point. Find: (a) the course and ground speed to the turning point; (b) the course and ground speed back; (c) the distance from the starting point to the turning point; (d) the time from the starting point to the turn.
Outline of Solution. Draw OC, Fig. 9, representing the velocity of the winrelative to the earth (evw = 15 mi. per hr.). From C describe two arcs of a circle of a radius (CD = CE) representing the speed of the plane relative to the wind (wvp = 60 knots). Draw lines CD and CE to the points at which these arcs intersect the ground course AB. Complete the parallelogram CG and CH. The course out is along the line OH and that back is along OG. The ground velocity (evp) is given by OE and the ground velocity back (evp') is represented by OD.
(a and b) The data of the problem give the magnitude 0H = OG together with the angles COB and COD. Using the law of sines and the law of cosines we find the values of P, 0', OE which represents the ground velocity out (evp), and OD which represents the ground velocity back (evp ).
(c) We have two expressions for the distance to the turning point: