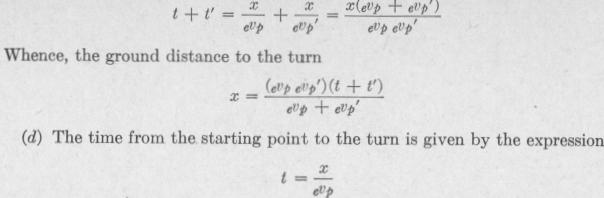10   PRINCIPLES OF ELEMENTARY DYNAMICS

where t represents the time occupied in going to the turning point and t' represents the time occupied in returning. Then, the time of the round trip

5. Composition and Resolution of Torques. - Three quantities are required to specify completely a torque. They are the magnitude of the torque, the direction of the torque-axis, and the sense in which the torque acts around that axis, that is, whether it is clockwise or counter-clockwise. A torque can be completely represented by a straight line of a length proportional to the magnitude of the torque, drawn in the direction of the torque-axis, and carrying an arrow-head so placed that on looking along the line in the direction of the arrow, the sense of the torque is clockwise.

The method of compounding concurrent torques is as follows: Draw from a given point two lines that represent the two simultaneous instantaneous torques. Complete a parallelogram on these two lines as sides. Then, the diagonal of the parallelogram drawn from the given point represents completely the resultant instantaneous torque.

6. Composition and Resolution of Angular Velocities, Accelerations and Momenta. - An angular velocity, an angular acceleration or an angular momentum can be represented completely by a straight line of a length proportional to the magnitude, drawn in the direction of the axis and carrying an arrow-head which indicates the sense of the angular quantity. In this book the arrow-head is so placed that, on looking along the line in the direction of the arrow, the sense of the angular velocity, acceleration or momentum is clockwise.

Angular velocities, angular accelerations and angular momenta are compounded and resolved by the parallelogram law exactly as are linear velocities and accelerations.

Experiment. - Set the Maxwell Top, shown in section in Fig. 10, into spinning motion when the point of support is (a) below the center of gravity of the top, (b) above the center of gravity. Ob-

TRANSLATION AND ROTATION

serve that the spin-axis of the body rotates in the direction of the spin when the center of gravity is above the point of support, and

in the direction opposite the

spin when the center of gravity is below the point of support. For each case make an angular momentum diagram showing the angular momentum at the beginning and end of a brief time interval and the change of angular momentum during this interval.

7. The Relation between the

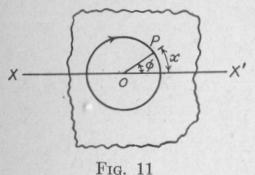
Angular Velocity of a Body and the Linear Velocity of Any Point of the Body. - Consider a body, Fig. 11, rotating with uniform angular velocity w about an axis through 0 perpendicular to the plane of the paper. Let XX' be a line fixed in space and PO a line fixed in the body perpendicular to the axis of rotation. If the body rotates steadily through the angle 0 in t seconds, then the angular speed is given, (1), by

where x represents the arc of radius r subtended by the angle ¢, and v represents the linear speed of the point P. This equati

shows that the angular speed of body equals the linear velocity of a point of the body divided by the dis tance of that point from the axis rotation.

8. The Relation between the Angu- lar Acceleration of a Body and the

Linear Acceleration of Any Point the Body. - If the body be acted upon by a torque, the angul velocity about the torque axis will change in t seconds from value wo to some value w,. The rate of change of angular velocit or the anular acceleration a, is