86   MOTION OF A SPINNING BODY

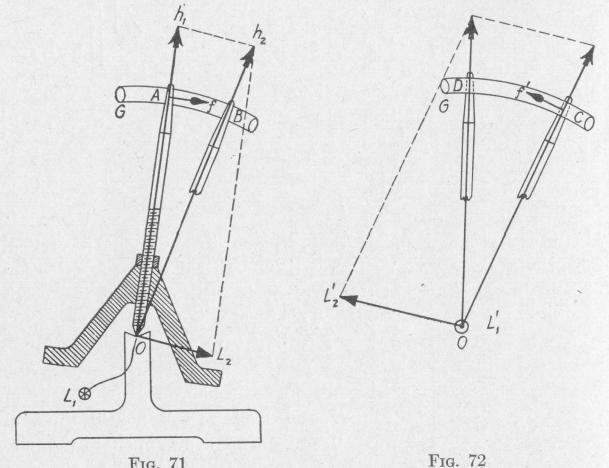
about the vertical axis. Pull the upper end of the axle over into contact with the guide G, and then release the axle. Now the end of the axle rolls or slides around against one side of the guide, clinging tightly to it, dashes around the end of the guide, still clinging to it, and rolls or slides along the other side of the guide.

Suppose that the top has an angular momentum about the spinaxis of constant magnitude. When the spinning axle is brought into contact with the guide there is developed on the axle a force of friction represented by the arrow f, Fig. 71. This force, in com

MOTION OF A SPINNING BODY   8i

of this force develops a torque acting on the axle represented by L2'. The spin-axle precesses from the position OC toward the position OD.

In this Article we have considered a spinning body with the fixed point coinciding with the center of mass of the body. Pressure is exerted also against the guide when the fixed point of the spinning body is either below or above the center of mass. An important application of this last case is made in the Griffin pulverizing mill, Art. 54.

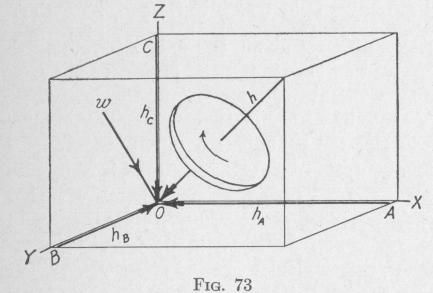
52. Components of the Torque Acting upon a Spinning Body Having one Fixed Point, Relative to the Three Coordinate Axes of a Rotating Frame of Reference. - In Fig. 73, the line h repre

bination with an equal, parallel, and oppositely directed force acting on the lower end of the axle, constitutes a torque L,. Under the action of this torque, the axle precesses against the guide and pushes against it with considerable force. The reaction of this force against the rotating axle, in combination with an equal, parallel, and oppositely directed force acting on the lower end of the axle, constitutes a second torque L2. Precession developed by this torque causes the upper end of the axle to slide along the guide

from the position A toward the position B.

When the axle is on the opposite side of the guide, the friction against the guide develops a torque acting on the axle represented by L,', Fig. 72. The axle presses against the guide. The reaction

sents the angular momentum of a spinning body. The axis of this angular momentum passes through the origin of a system of coordinate axes OABC. The components of h about the axes of this reference frame are hA, hB and hc, respectively. Let this reference frame OABC be capable of rotation with angular velocity w about an axis through the origin 0 of a set of rectangular axes OXYZ, fixed in space. Denote the projections of w on the axes of the rotatable frame by WA, WB and wc, respectively. It is required to find expressions for the torque, that is the rate of change of the angular momentum of the given body, at any instant, with respect to the moving axes OA, OB and OC.

The torque acting on the spinning body about the axis OA, at any instant, is made up of the sum of four parts - the rate of change of the angular momentum about the axis OA of the angular momentum h if the movable frame were at rest relative to the fixed frame of reference, and the three torques about the axis OA