184   NAVIGATIONAL COMPASSES

Problem. - A ship at latitude 60° N. is steaming north-east with a speed of 20 knots. Find the deflection of the spin-axle of the gyro-compass from the geographical meridian due to the meridian-steaming error.

Solution. - From (119), since 0 = 45° and a = 60°,

S, = 0.06320 (00.507) V.8 _   west of the meridian

112. The Deflection of the Axle of a Gyro-Compass Produced

by Acceleration of the Ship's Velocity. The Ballistic Deflection

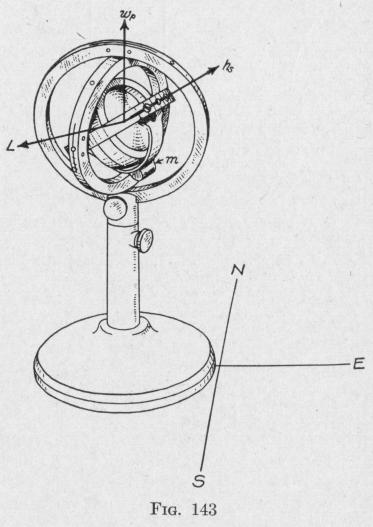
Error. Experiment. - The pivots supporting the inner frame of the gyroscope, Fig. 143, are horizontal. A mass m attached rigidly to this frame and hanging below the gyro-wheel tends to keep the gyro-axle horizontal when the frame is at rest. Place the gyroscope on the intersection of two lines drawn at right angles to one another on the table, and marked S-N and W-E, respectively. Place the spin-axle parallel to the S-N line, and set the gyrowheel spinning in the direction indicated by the

arrow h.

(a) Slide the instrument quickly along the table in the direction

S-N. During the time the motion of the frame is being accelerated

in the direction S-N, the pendulous mass m hangs back, thereby

developing a torque about an axis parallel to the E-W line in the

direction indicated by the arrow L. The spin-axis turns toward

the torque-axis about a vertical axis in the direction represented by the arrow wp.

(b) Accelerate the motion of the gyro-frame in the direction N-S or decelerate the motion in the direction S-N. Note that during the change in velocity the spin-axle precesses in the direction opposite that developed in the preceding case (a).

NATURAL ERRORS   185

(c) Push the gyroscope in the direction S-N with constant velocity and then suddenly move it toward either the right or left. Note that, during the change in the direction of the velocity, the spin-axle precesses in the same direction as in case (b) when the motion in the direction S-N was decelerated.

(d) Now accelerate the motion of the gyro-frame in either the direction E-W or W-E, that is, perpendicular to the spin-axis. No change in the direction of the spin-axis is produced.

Question. Suppose that we have a non-pendulous mercury ballistic gyrocompass with the spin of the gyro in the direction opposite that considered above. Find the direction of the deflection of the spin-axle that would be

produced if the instrument were to be accelerated in each of the ways considered above.

So long as the velocity of a ship is constant, the spin-axle of the gyro-compass will have a resting position at a small angle from the meridian of a magnitude depending upon the velocity and latitude of the ship (Arts. 110 and 111). If the velocity of the ship is changing while the ship is on any heading except perpendicular to the spin-axle of the gyro-compass, then during the time the velocity is changing, the spin-axle will be deflected from the resting position which the spin-axle had when the ship was moving with its first velocity. This deflection will be constant while the acceleration remains constant. The deflection of the spin-axle from its resting position, produced by an acceleration of the meridian component of the ship's velocity, is called the ballistic deflection.

A diminution of velocity in the meridian is produced not only by diminishing the speed in the meridian but also by changing the heading either eastward or westward. In every case, the ballistic deflection produced by any acceleration of the ship's velocity is in the same direction as the change in the direction of the resting position of the gyro-axle, on account of the changing meridiansteaming error.

Consider a ship steaming north at 10 knots. Because of the meridian-steaming error, the resting position of the spin-axle will be at an angle NOX, west of the meridian, Fig. 144. Suppose that now the speed on the same heading be increased to 20 knots. The resting position of the spin-axle corresponding to the new velocity is shifted to YO. Suppose that during the time the speed was changing from 10 knots to 20 knots, the ballistic torque acting on the gyro-frame caused the gyro-axle to precess into the position