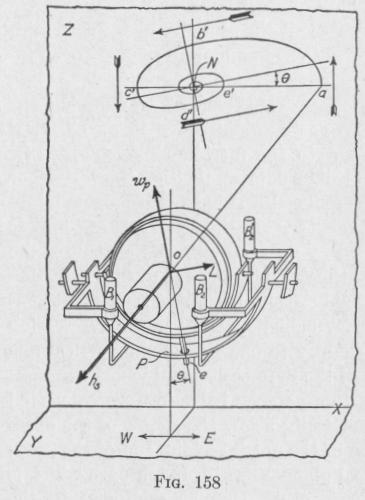
204   NAVIGATIONAL COMPASSES

nearer the horizontal than it would if the precession axis were vertical, Fig. 158. It will cross the horizontal at a point c' nearer the meridian than it would if the precession axis were vertical. It will cross the meridian again at a point d' nearer the horizontal than it would if the precession axis were vertical. In fact, the prolongation of the north-seeking end of the spin-axle traces on a vertical plane XZ, perpendicular to the meridian plane, a spiral that converges to a point on this plane very close to the intersection of the meridian and the horizontal plane through

the center of mass of the gyro. When the compass is in northern latitudes, this point is slightly above the horizontal; when in southern latitudes, it is slightly below. The principal axis of the spiral is inclined to the horizontal plane and is fixed with reference to the precessing gyro-wheel. The degree of damping is controlled by the distance between the pin e and the vertical through the center of the gyro. The amplitude of each swing of the gyro-axle is about one-third that of the preceding swing.

In Fig. 158, the torque

acting on the gyro-wheel is represented by L. This torque produces a precessional velocity represented by wp, toward h'. If the mercury ballistic is maintained always in the same position relative to the gyro-axle, then the projection of the gyro-axle will continue to leave the elliptical path and trace a converging spiral having a major axis inclined to that of the ellipse. The constancy of the position of the mercury ballistic relative to the gyrowheel is maintained by means of the follow-up system. This causes the ballistic to follow every movement in azimuth of the spin-axle. By means of the ballistic, supported by the phantom, and the eccentric connection, with the gyro-case and mer-

THE SPERRY GYRO-COMPASS   205

cury ballistic, the spin-axle will quickly settle to a position which is nearly horizontal and in the geographic meridian.

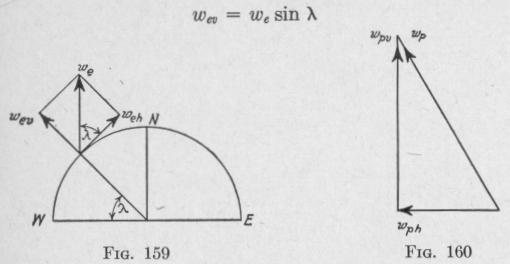
122. The Magnitude of the Latitude Error for Which Correction Must Be Made in the Sperry Gyro-Compass. - When the gyro-compass is at any latitude there is a vertical component of the earth's angular velocity we of the value, Fig. 159,

It follows that, in order that the spin-axle may remain in the meridian, the spin-axle must be caused to precess about a vertical axis with an angular velocity equal in magnitude to we„ but in the opposite direction. This precession requires a torque about a horizontal axis. The requirement of a torque about a horizontal axis, and the additional requirement that for damping there must at the same time be a torque about the vertical axis, are fulfilled in the Sperry Mark V compass and later models by connecting the mercury ballistic to a point of the gyro-casing slightly to the east of the point vertically below the center of the gyro-wheel, as we have seen in Arts. 107 and 121. By this scheme, the applied torque is about an axis making a small angle 0 to the horizontal, and the precessional velocity wp thereby produced is about an axis inclined at the angle 0 to the vertical.

The horizontal component of the torque produces a precessional velocity wp, about a vertical axis, Fig. 160. The vertical component of the torque produces a precession wph about a horizontal axis perpendicular to the gyro-axle of the value

wph = wp, tan 0

If the spin-axle of the compass is to remain in the meridian, the vertical component of the velocity of precession must equal the vertical component of the earth's rotation. That is,

Wp, = w,