TRANSLATION AND ROTATION 13
where a represents the tangential component of the linear acceleration of a point distant r from the axis of rotation. Thus, in words, the tangential component of the angular acceleration of a body equals the linear acceleration of any point of the body divided by the distance of that point from the axis of the acceleration.
9. Centripetal and Centrifugal Force. - It is readily shown* that, when a body is acted upon by a force of constant magnitude having a line of action always in the same plane and always perpendicular to the direction of the motion, (1) the speed of the body does not change, (2) the path of the body is a circle, (3) the body is moving with a linear acceleration which is always directed toward the center of the circle, and (4) the magnitude of this radial acceleration is constant and equal to the square of the linear speed of the body divided by the radius of its path.
According to Newton's First Law of Motion, a moving body will continue to move in a straight line with constant speed until acted upon by an external force. From the preceding paragraph, when a body of mass m moves with constant speed v in the circumference of a circle of radius r, we see: (1) that there must be a force acting upon the body, (2) this force must be directed toward the center of the circle, and (3) the magnitude of the force is given by
The force required to overcome the inertia of a body in deflecting it from a rectilinear path into a circular path is called centripetal force. The agent which constrains the body to move in a circular path is acted upon by a force directed away from the center of the circle and has a magnitude equal to the force acting upon the body that is moving in the circular path. This, frequently called centrifugal force, is the reaction of the centripetal force and may be defined as the resistance which the inertia of a body in motion opposes to whatever deflects it from the rectilinear path. The centripetal force acts upon the body that is moving in a circular path, and its reaction, the centrifugal force, acts, not upon this body, but upon the agent which constrains it to move in a circular path.
10. The Dynamic Vertical and the Dynamic Horizontal. - A plumb-bob that is at rest or in uniform linear motion relative to the earth indicates the direction of the force of gravity at the
* Ferry's General Physics, Art. 66.
place where it is situated. This direction is the true vertical. When a plumb-bob is moving with a linear acceleration relative to the earth, it assumes a direction called the dynamic vertical corresponding to the given linear acceleration.
A plane normal to the true vertical is called a true horizontal. A plane normal to a dynamic vertical is called a dynamic horizontal corresponding to the given linear acceleration. The free surface of an unaccelerated liquid is truly horizontal. The free surface of a liquid in a vessel moving with linear acceleration is not truly horizontal. When the speed of a locomotive is increasing, the water gauge gives an indication that is too high; when the speed is decreasing, the indication is too low. The free surface of water in a rotating vessel is not truly horizontal.
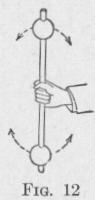
11. Moment of Inertia. Experiment. - With the arm outstretched, rotate back and forth an iron pipe on which are mounted
two iron balls, Fig. 12. Note that a considerable torque, produced by twisting the wrist, must be given the rod to change quickly the angular velocity, whereas a smaller torque is required to produce a smaller angular acceleration. Note that when the spheres are close to the hand, a fairly small torque, produced by twisting the wrist, will impart to the apparatus a certain angular acceleration about the outstretched arm as an axis. When the spheres are
at a distance of a foot or more from the hand, a much larger torque is required to produce the same angular acceleration.
That property of a body because of which a torque is needed to give the body an angular acceleration is called moment of inertia. When a torque acts upon a body, it produces an angular acceleration that is directly proportional to the torque and inversely proportional to the moment of inertia of the body upon which it acts. The moment of inertia is to be taken about the axis of the torque. The angular acceleration is about the same axis. Or,
in symbols,
The moment of inertia K of a body consisting of particles of masses m,, m2, m3, etc., at distances r,, r2, r3, etc., respectively, from the axis of rotation is