16   PRINCIPLES OF ELEMENTARY DYNAMICS

any other axis through the same point if the length of the cylinder is greater than the diameter. The moment of inertia of the cylinder about an axis through the center of mass and in the direction of the length is less than that about any other axis. In the case of most bodies, the values of the moments of inertia relative to their mutually perpendicular axes are unequal.

It can be shown that the axis of greatest and that of least moment of inertia are perpendicular to one another. The perpendicular axis through the center of mass of a body about which the moment of inertia is maximum, that about which it is minimum, and the other axis perpendicular to these two, are called the principal momental axes of the body. The moments of inertia about the principal momental axes are called the principal moments of inertia of the body. If the principal moments of inertia of one body or system are equal, respectively, to the principal moments of inertia of another body or system, the two bodies or systems are said to be equimomental.

For any rigid body there can be constructed an equimomental system consisting of three slender and uniform rigid rods bisecting each other at right angles, and coinciding in direction with the principal momental axes of the given body.

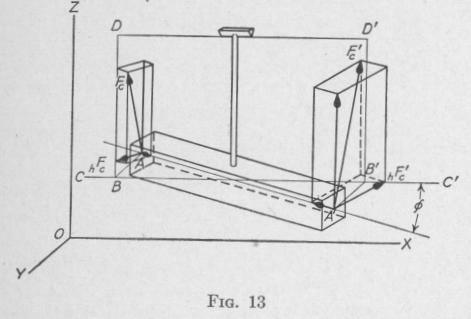
14. Centripetal Forces Acting upon an Unsymmetrical Pendulum Bob. - Consider a pendulum having a bob that is capable of rotation with negligible friction about the axis of the pendulum rod and that is unsymmetrical with respect to the axis of the pendulum rod. In Fig. 13, the pendulum bob is a rectangular bar with the long axis perpendicular to the pendulum rod. The long axis of the bob is inclined at an angle 0 to the plane of the knifeedge and the pendulum rod. Consider A and A' at the centers of the two ends of the bob at the instant when the pendulum is passing through the equilibrium position. From A and A' draw lines A B and A'B' perpendicular to the line CC' through the center of the bob parallel to the knife-edge. From B and B' draw lines BD and B'D' perpendicular to the knife-edge. The points D and D' are the points about which oscillate the two particles at A and A'.

In order that the particles at A and A' may rotate about DD', the particles must be acted upon by centripetal forces F, and F,' directed toward D and D', respectively. Each of the centripetal forces F,, etc., can be resolved into three components, one vertical, one parallel to the axis of the bob, and one horizontal and per

TRANSLATION AND ROTATION   17

pendicular to that axis. In the diagram, the horizontal components acting on the particles A and A', perpendicular to the

axis of the rod, are marked hF, and 1,F,', respectively. The hori

zontal force acting on each particle necessary to cause the bob to swing so that the long axis is inclined at an angle 0 to the plane through the knife-edge and pendulum rod is non-existent when there is zero friction between the bob and the pendulum rod. If these horizontal forces are non-existent, the inertia of each particle

of the bob will cause it to retreat as far as possible from the line CC'. Therefore the stable position of the loose bob is attained when the long axis of the bob is perpendicular to the plane of the knifeedge and pendulum rod.

An oscillating body tends to set itself in the position in which its moment of inertia with respect to the vibration axis is maximum. A body having equal principal moments of inertia will oscillate in any plane through the center of mass without any tendency to turn.

Similarly, if a body, supported at the center of mass so as to be capable of turning in any direction, be moved in a curved path, the body will tend to turn so that the axis of minimum moment of inertia is tangent to the path. A body that has equal principal moments of inertia has no tendency to turn when moving in a curved path.

15. The Relation between Torque and Angular Momentum. - The product of the moment of inertia of a body K, with respect to an axis through a point c, and the angular velocity w, about the same axis, is called the angular momentum of the body with respect