Applied Gyrodynamics - A 1932 book on gyroscopes and gyroscope based apperatus

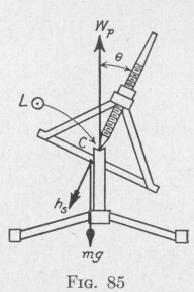
106 THE GYROSCOPIC PENDULUM

sented by h,. The precessional velocity wp is about a vertical axis. If the inclination of the spin-axle to the vertical be represented by 0, then the external torque L is given by

L = mgl sin 0

From the Second Law of Gyrodynamics, Art. (34), this external torque equals the product of the precessional velocity and the component of the angular momentum about an axis perpendicular to the torque-axis and the precession axis. Thus

mgl sin 0 = wph, sin 0

Hence the precessional velocity _ mgl WP h,

The period of the precessional motion, that is the period of the gyroscopic conical pendulum

T[= 2 7r] = 2 irh, (80) WP mgl

If the radius of gyration of the precessing system, with respect to the spin-axis, be k,, the above expression may be put into the forms

T 2 irh, _ 2 irK,w, - 2 7rk,2w, (81)

mgl ] mgl gl

The length of a simple pendulum of the same period, from (51), (80), and (81) is

l-T2 g - -h,2 = k,'w,2

47r2 m212gg12

(82)

67. The Inclination of the Precession Axis of a Gyroscopic Conical Pendulum to the Vertical. - A spinning gyro on the earth has two component angular velocities, one w„ about the spin-axis of the gyro, and another, wej about the axis of the earth. The centrifugal couple tending to bring the spin-axis into parallelism with the axis of the earth is about an axis perpendicular to the plane of the spin-axis and the axis of the earth. The axis of the resulting precession is inclined to the vertical at a small angle now to be determined.

In Fig. 86, the point G represents the center of mass of a gyro on the earth at latitude X; the line AG is the spin-axis of the gyro

GENERAL PROPERTIES 107

and D is the point of support; the line VC is the true vertical and H H' is the true horizontal at G; the line NS is parallel to the axis of the earth. The spin-axis is inclined to the axis of the earth at an angle 0.

The gyroscopic torque has the magnitude given in (58). It also equals the product of some force GF parallel to the axis of the earth and a lever arm DQ[= DG sin 0].

Or hswe sin 0 = GF(DG sin 0)

Whence, the force parallel to the earth's axis has the value

GF = hl se (83)

where 1 represents the distance DG.

The gyro is also acted upon by

its weight mg, represented in the figure by the line GW. The resultant GR of the two forces GF and GW is the apparent force of gravity acting on the gyro. Its direction is the apparent vertical about which the gyro-axle pre

cesses. The angle i between the true vertical VC and the axis V'R about which the gyro-axle precesses is given by the equation

GJ _ GF cos X

tan i L JR] JF + FR

Since i is very small, we may write tan i = i. Since JF is very small, compared to FR(=GW), it may be neglected and the above equation may be written

_ GF cos A

i (84)

From (83), this becomes

_ hswe COS X

i l

Now the external torque acting on the gyroscope is mgl sin 0, where 0 is the angle between the spin-axis and the vertical. The component of the angular momentum about an axis perpendicular