108   THE GYROSCOPIC PENDULUM

to the vertical is h5 sin c. Hence, from the Second Law of Gyrodynamics, (Art. 36),

mgl sin 0 = hswp sin 0

Substituting the value of mgl from this equation in (84), we obtain for the angle between the precession axis and the vertical

we cos A

i =      (85)

WP

The angular velocity of the earth

we = 2 a radians [   per day]    2'r

86,400 radians per sec. and the angular velocity of precession

wp = T radians per sec.,

where T represents the period of precession.

Substituting in (85) these values of we and wp, and remembering that

1 radian = 3438 minutes of angle, = T cos X   r T cos A (3438)

2   86,400    radians L =   86,400    minutes

T cos a minutes of arc (86)

25.14

Thus, when the period of precession is 25.14 seconds of time, the

angle i at the equator is one minute of arc.

68. The Period of the Undamped Vibration, Back and Forth Through the Meridian, of the Gyro-Axle of a Pendulous Gyroscope. - Figure 87 represents the gyro-axle AO of a pendulous gyroscope referred to rectangular coordinate axes OV, ON, and OE that extend vertically upward, northward and eastward. The gyro-axis is in the vertical plane VOH. It is inclined to the meridian plane VO N at the angle 0 and

to the horizontal plane EON at the angle 0. The center of mass

of the gyro and frame is at G and the point of suspension of the

moving system is at D. The distance DG will be represented by

the symbol 1. The gyro-axis A 0 and the line DG are perpendicu

GENERAL PROPERTIES   109

Jar to one another. The weight mg of the moving system has a lever arm BG about an axis through D perpendicular to the plane VO H and produces a torque about this axis of the value L = mgl sin 0.

Representing the angular velocity of the moving system about a vertical axis 0 V fixed in space by w', and the angular momentum of the gyro-wheel with respect to a horizontal axis OH by he', then when the precession is steady we have

L = hs'w'

Since the velocity of precession of the moving system about a vertical axis fixed to the earth is do/dt, the velocity of precession

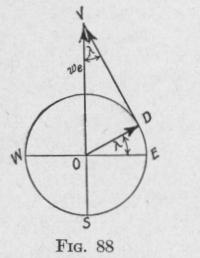
about a vertical axis fixed in space equals the sum of det/dt and the component velocity of the earth about the vertical at the given place. If we represents the angular velocity of the earth about its axis, then the component angular velocity OD, Fig. 88, about a vertical axis through a point D at latitude A is we sin X. Hence the velocity of precession about a vertical axis fixed in space is

W' = d + we sin A

The component of hs about OH perpendicular to OV, Fig. 87, is

hs' = hs cos 0

Consequently, for an axis fixed in space through D and perpendicular to the vertical plane VO H,

[L =] mgl sin 0[= hs'w'] = It, cos O(d-0+ we sin a)

When 0 is so small that the difference between cos 0 and unity may be neglected and also the difference between sin 0 and 0 radians, we may write

mgl 0 = hs (dt + we sin X)

(87)

The left-hand side of this equation is the gravitational torque which tends to cause the gyro-axle to become horizontal. The right-hand side is the gyroscopic resistance offered by the gyroaxle opposing the tendency to dip.

Again, the velocity of precession about a horizontal axis 0H', or NH, Fia. 87, fixed to the earth and perpendicular to the spin-